
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
М(t) = М(cos t; sin t). Значения тригонометрических функций некоторых углов. Связь между тригонометрическими функциями одного аргумента. Искомая функция. Выражение искомой функции через
М(t) = М(cos t; sin t)
 |
Запись М(t) показывает положение точки М на координатной окружности, а запись М(cos t; sin t) – положение той же точки на координатной плоскости.
Функция тангенс — это частное от деления функции синус на функцию косинус.
Функция котангенс — это частное от деления функции косинус на функцию синус.
 |
Поскольку деление на нуль невозможно, функции tg t и ctg t определены не для всех значений аргумента. Тангенс определен лишь для значений аргумента, при которых cos t ¹ 0, котангенс определен при sin t ¹ 0:
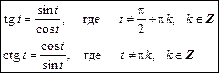
Тригонометрические функции — это общее название функций синус, косинус, тангенс и котангенс.
I. Основное тригонометрическое тождество и следствия из него:

II. Формулы (теоремы) сложения аргументов:
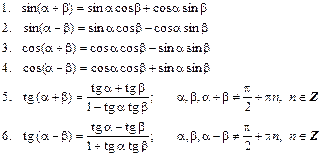
III. Формулы приведения:
1) функция меняется на кофункцию при переходе через вертикальную ось и не меняется при переходе через горизонтальную;
2) перед приведенной функцией ставится знак приводимой функции, считая a углом первой четверти.
IV. Формулы двойного аргумента:
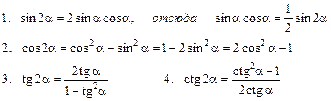
V. Формулы понижения степени:

Значения тригонометрических функций некоторых углов
таблица 1
| p | |||||||
| sin a | 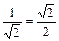
| 
| –1 | ||||
| cos a | 
| 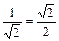
| –1 | ||||
| tg a | 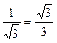
| 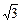
| — | — | |||
| ctg a | — | 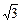
| 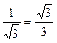
| — |
Связь между тригонометрическими функциями одного аргумента
таблица 2
|
Искомая функция |
Выражение искомой функции через | |||
| sin a | cos a | tg a | сtg a | |
| sin a = | sin a | 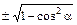
| 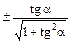
| 
|
| cos a = | 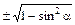
| cos a | 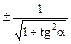
| 
|
| tg a = | 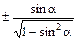
| 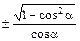
| tg a | 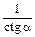
|
| сtg a = | 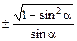
| 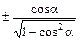
| 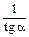
| сtg a |
|

Тригонометрический набор координат:
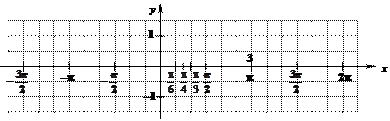 |
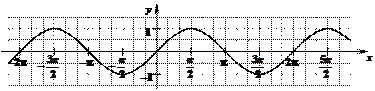 у = sin x синусоида
у = sin x синусоида
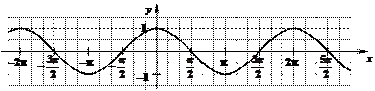 у = cos x á ко ñ синусоида
у = cos x á ко ñ синусоида
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|