Задание 1.9. Задание 1.13? (1.14?)

Задание 1. 9

Величина электрического поля, создаваемого элементом заряженной поверхности диска в произвольной точке на оси, дается выражением

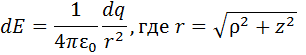
r – радиус-вектор элемента поверхности в цилиндрической системе координат.

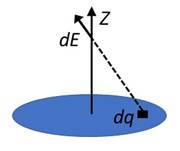
В силу очевидной осевой симметрии задачи итоговое поле, создаваемое всем диском будет направлено вдоль оси Z. Поэтому нас будет интересовать не величина поля, а величина проекции поля на эту ось.

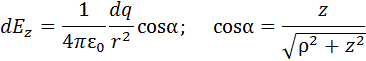
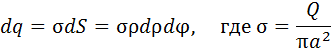
Полное поле находим интегрированием по r от 0 до a и по углу от 0 до 2p. В результате получаем величину поля, направленного вдоль оси Z.

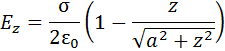
Как часто бывает в физических задачах, полезно проанализировать это выражение в предельном случае ( 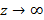). Поделим числитель и знаменатель дроби в скобках на z и тем самым образуем малый параметр a/z. Используя разложение в ряд Тейлора с точностью до членов первого порядка малости, получим

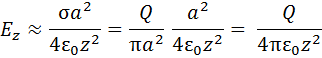
Результат понятен: на больших расстояниях (существенно больших размеров диска) сам диск создает поле практически равное полю точечного заряда, то есть распределение заряда по диску в этом предельном случае роли не играет, " работает" полный заряд.

Задание 1. 13? (1. 14? )

Задачу трудно решить прямым интегрированием, но она достаточно просто решается методом дополнения, который будет применен при рассмотрении и других задач этого курса.

Мысленно дополним шар с полостью малым шаром радиуса r с объемной плотностью заряда r. Таким образом, образуем однородный большой шар. По принципу суперпозиции поле, создаваемое несколькими объектами в какой-то точке пространства, является векторной суммой полей этих объектов в этой точке. После произведенного дополнения поле в произвольной точке А внутри полости можно рассматривать двояко.

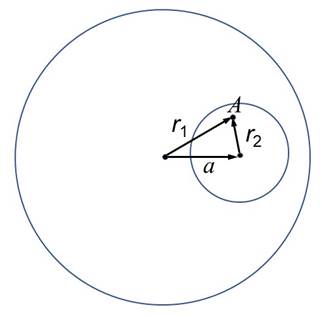
Во-первых, это поле можно рассматривать как поле в произвольной точке внутри однородно заряженного большого шара:

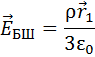
Во-вторых, можно воспользоваться принципом суперпозиции и считать, что поле в точке А равно векторной сумме поля, создаваемого малым шаром

и поля большого шара с вырезанной в нем полостью (искомого поля) .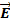

Поскольку мы по-разному описали одно и то же поле, то справедливо соотношение

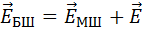
Тогда

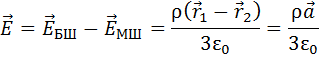
Таким образом, внутри сферической полости, находящейся внутри равномерно заряженного шара, создается однородное(! ) электрическое поле, не зависящее от радиусов шара и полости(! ).

Домашнее задание

1. 2

1. 5

1. 6

1. 10

1. 16? (1. 17? ) Бесконечная прямолинейная полоса шириной 2l…

⇐ Предыдущая 12