Решение

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

1. Определение реакций в опорах. Уравнения равновесия:

Σ m_A = 0; -F1 · 6 + m- R_B · 10 + F₂ · 12 = 0; -35 · 6 + 80 - R_B · 10 + 70 · 12 = 0;

250 Лекция 30

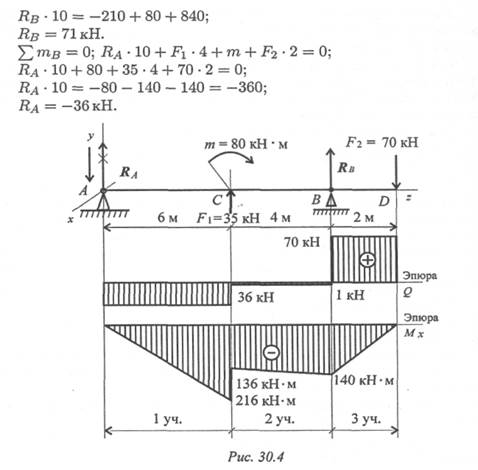
Реакция в опоре направлена в обратную сторону.

Проверка: Σ Fy = 0;

-R_A + F1 + R_B - F₂ = 0; -36 + 35 + 71 - 70 = 0.

Реакции определены верно.

2. Для упрощения расчетов при построении эпюр поперечных сил и изгибающих моментов можно провести расчет по характерным точкам без составления уравнений.

Для этого используют известные связи между поперечной силой и изгибающим моментом и правила построения эпюр. -

Участок 1 (от точки А до точки С).

Тема 2. 6. Изгиб 251

В точке А приложена реакция Ra, направленная вниз. Поперечная сила на участке постоянна: Q1 = Ra = - З6кН.

Момент в точке А равен нулю.

Точка С (слева). Приложена внешняя сила F1 = З5кН, направленная вверх, — здесь возникнет скачок вверх на величину З5кН. Момент в точке С (слева) может быть рассчитан по известной зависимости МС^слева =-R_A · 6; МС^слева=-36·6 =-216 кН· м.

Участок 2 (от точки С справа до точки В).

Поперечная сила в точке С (справа) равна Qc = -Ra + F1; Q_c = -36 + 35 = -1кН.

В точке С приложена внешняя пара сил с моментом 80кН·м, следовательно, здесь проявляется скачок на величину приложенного момента: Мc^справа = МС^слева+ m; Мc^справа = -216 + 80 = 136кН·м.

Поперечная сила на втором участке постоянна: Q2 = Qc^справа.

Момент в точке В определяется по зависимости

МB = -R_A • 10 + F1 • 4 + m; M_B = -36 • 10 + 35 • 4 + 80 = -140 кН•м.

Справа и слева от точки В момент имеет одинаковые значения.

Участок 3 (от точки В (справа) до точки D).

В точке В приложена внешняя сила Rb. Здесь появляется скачок на величину 71 кН, Q_B = -1 + 71 = 70 кН.

Дальше по участку поперечная сила не изменяется. Момент в точке D равен нулю, т. к. здесь не приложена внешняя пара сил: M_D = 0.

Рассмотрение поперечных сил и изгибающих моментов можно было провести и справа налево.

По полученным значениям сил и моментов строим эпюры (эпюры под схемой вала, рис. 30. 4).

⇐ Предыдущая 123 Следующая ⇒