
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Ответ. 1.. Решение.. Ответ. у = 4х – 7.. Самостоятельная работа.. Вариант4
Ответ. 1.
Пример 2. Найдем уравнение касательной к графику функции f(x) = x3 – 2x2 + 1 в точке с абсциссой  .
.
Решение.
Следуем алгоритму.
1) Точка касания xоравна 2. Вычислим f (xо): (подставим 2 вместо x в данную функцию)
f(xо) = f(2) = 23 – 2 ∙ 22 + 1 = 8 – 8 + 1 = 1
2) Находим f′ (x). Для этого находим сначала производную:
f′ (x) = 3х2 – 2 ∙ 2х = 3х2 – 4х.
Теперь в это выражение подставляем вместо x= 2, это и будет f ′ (xо):
f′ (xо) = f′ (2) = 3 ∙ 22 – 4 ∙ 2 = 12 – 8 = 4.
3) Итак, у нас есть все необходимые данные: xо= 2, f(xо) = 1, f′ (xо) = 4. Подставляем эти числа в уравнение касательной и находим окончательное решение:
у = f(xо) + f′ (xо) (x – xо) = 1 + 4 ∙ (х – 2) = 1 + 4х – 8 = –7 + 4х = 4х – 7.
Ответ. у = 4х – 7.
Самостоятельная работа.
Вариант 1: Антонова Ю., Ильина Ю., Громов А., Каримов Р., Сухарева С.
Вариант 2: Козлицкая Е., Козлицкая Е., Трошкина А., Киясова В., Сагидуллина Ю.
Вариант 3: Колобова А., Мерцалова А., Насырова Г., Римеева П., Гордиенко В.
Вариант 4: Сайфутдинова М., Сулейманов Д., Хисматьуллин Р., Фахретдинова Э., Хабибуллин В., Шаяхметов С.
| № | Вариант1 | Вариант2 | Вариант3 |
Вариант4 | |
| Прямаяпараллельна касательной к графику функции y=f(x). Найдите абсциссу точки касания. (по примеру 1) | |||||
| y = -6x-2, y = 3x2 -12x+7 | 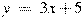 , , 
| y=-5x+2, y = 3x2+7x+1 | y=4-3x, y = 2x2-x-12 | ||
| Составьте уравнение касательной к графику функции y=f(x) в точке x0. (смотрите пример2) | |||||
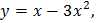

| 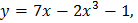

| 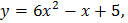

| 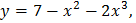

| ||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|