
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры и разбор решения заданий тренировочного модуля
№1. Материальная точка движется прямолинейно со скоростью v(t)=8t–4. Найдите закон движения точки, если в момент времени t=2c пройденный путь составил 4 м.
Решение:
Воспользуемся определением первообразной, т. к. S(t)=v0t+at2/2
S’(t) = v(t).
Найдем все первообразные S(t)= -4t+4t2 +c.
Подставим t=2c и пройденный путь S=4 м.
4= -8+16+с
С= -4.
Следовательно, закон движения будет выглядеть следующим образом:
s(t)=4t2–4t–4
Ответ: s(t)=4t2–4t–4
№2. По графику первообразной функции y = F(x) определите количество точек, в которых функция y = f(x) равна нулю.
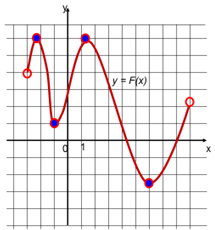
Решение:
Так как F'(x) = f(x) -по определению первообразной, то точки, в которых функция f(x) (производная функции F(x)) – это точки экстремума функции F(x). А таких точек на графике 4.
Ответ: 4.
№3. По графику первообразной функции y = F(x) определите числовые промежутки, на которых функция y = f(x) имеет отрицательный знак.
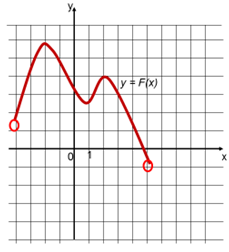
Решение:
Так как F’(x) = f(x)- по определению первообразной, то числовые промежутки, на которых функция f(x) (производная функции F(x)) имеет отрицательный знак – это промежутки убывания функции F(x). Таких промежутков на данном графике 2. Это (-2; 1) и (2; 5).
Ответ: (-2; 1); (2; 5).
№4. Докажите, что функция y = F(x) является первообразной для функции y = f(x).
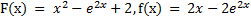
Решение:
Доказательство.
F'(x)=(х2-е2х+2)'=2х-2е2х
По определению первообразной, F'(x)=f(x), следовательно, F'(x) и есть первообразная для функции f(x)
№5. Для функции f(x) = х 2 найти первообразную, график которой проходит через точку (-3; 10).
Решение:
Найдем все первообразные функции f(x): 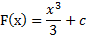
Найдем число С, такое, чтобы график функции f(x) = х 2 проходил через точку (-3; 10). Подставим х = – 3, y = 10, получим:
10 = (-3)3/3 +с
С=19
Следовательно, 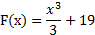
Ответ: 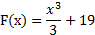
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|