
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №3
Тема: Выполнение расчетов по использованию законов термодинамики
Цель: Изучить основные термодинамические процессы, сформировать умение выполнять расчеты с использованием основных законов термодинамики
Оснащение : Методические указания для выполнения работы. Варианты заданий.
Литература:
1. В. Н. Луканин. Теплотехника. Москва, Высшая Школа, 2009 г
2. Ерофеев В. Л., Семенов П. Д., Пряхин А. С. Теплотехника. Москва, Икц «Академкнига», 2008 г.
3. В. Г. Ерохин, М. Г. Маханько. Сборник задач по основам теплотехники и гидравлики. Москва, Энергия, 1972 г.
Контрольные вопросы:
1. Дайте понятия удельной, массовой и киломольной теплоёмкости. Приведите их обозначения и размерности.
2. Как определить работу термодинамического процесса?
3. Какие существуют соотношения между теплоёмкостями при постоянном давлении и объёме?
Порядок выполнения работы:
1. Изучаем методические рекомендации к работе.
2. Знакомимся с примерами решения заданий.
3. Выписываем необходимые для решения заданий формулы.
4. В соответствии с вариантом задания производим расчеты.
5. Делаем выводы.
Краткие теоретические сведения
Уравнения состояния идеальных газов записывают:
– для 1 кг газа
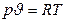 , (1. 1)
, (1. 1)
– для m кг газа
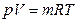 , (1. 2)
, (1. 2)
– для 1 моль газа
 , (1. 3)
, (1. 3)
где 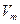 – молярный объем, м3/моль;
– молярный объем, м3/моль; 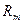 – универсальная (молярная) газовая постоянная, Дж/(моль К).
– универсальная (молярная) газовая постоянная, Дж/(моль К).
Универсальная газовая постоянная 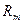 = 8, 314 Дж/(моль. К).
= 8, 314 Дж/(моль. К).
Удельная газовая постоянная, Дж/(кг К),
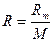 , (1. 4)
, (1. 4)
где 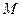 – молярная масса, кг/моль.
– молярная масса, кг/моль.
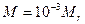 , (1. 4а)
, (1. 4а)
где 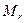 – относительная молекулярная масса вещества.
– относительная молекулярная масса вещества.
Термодинамическая температура, К,
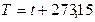 , (1. 5)
, (1. 5)
где 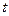 – температура в градусах Цельсия, 0С.
– температура в градусах Цельсия, 0С.
Принято приводить объем газа к так называемым нормальным условиям, при которых давление газа 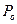 = 101, 3 кПа, а температура
= 101, 3 кПа, а температура  = 0 0С.
= 0 0С.
Смеси идеальных газов подчиняются законам идеальных газов. Газ (компонент) в составе смеси сохраняет свои свойства и ведет себя так, как если бы он один занимал весь объем смеси. Каждый компонент находится под своим парциальным давлением.
Давление газовой смеси
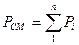 , (1. 6)
, (1. 6)
где 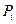 – парциальное давление компонента.
– парциальное давление компонента.
Состав газовой смеси может быть задан массовыми и объемными (молярными) долями.
Если массовая доля представляет собой отношение массы компонента к массе газовой смеси, то объемная доля – отношение парциального объема компонента к объему газовой смеси. Парциальный объем компонента приведен к температуре и давлению газовой смеси.
Для газовой смеси 
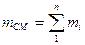 , (1. 7)
, (1. 7)
где 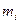 – масса компонента;
– масса компонента;
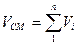 , (1. 7а)
, (1. 7а)
где 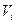 – парциальный (приведенный) объем компонента, м3.
– парциальный (приведенный) объем компонента, м3.
Плотность газовой смеси
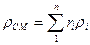 , (1. 8)
, (1. 8)
где 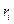 – объемная доля компонента;
– объемная доля компонента; 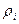 – плотность данного компонента, кг/м3;
– плотность данного компонента, кг/м3;
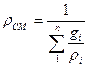 , (1. 8а)
, (1. 8а)
где 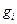 – массовая доля компонента.
– массовая доля компонента.
Кажущаяся молярная масса смеси идеальных газов
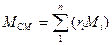 , (1. 9)
, (1. 9)
где 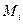 – молярная масса компонента;
– молярная масса компонента;
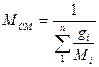 . (1. 9а)
. (1. 9а)
Удельную газовую постоянную рассчитывают по формуле (1. 4) с использованием кажущейся молярной массы.
Соотношение между массовыми и объемными долями
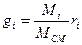 . (1. 10)
. (1. 10)
Парциальное давление компонента
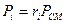 . (1. 11)
. (1. 11)
Молекулярные массы и удельные газовые постоянные некоторых газов приведены в приложении Б.
Теплоемкость определяет количество теплоты, которое необходимо подвести к телу (к системе), чтобы повысить температуру на 1 0С (на 1 К).
Теплоемкость относят к единице массы, к единице объема и к единице количества вещества. Соответственно различают удельную, объемную и молярную теплоемкости, (обозначения 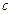 ,
, 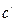 , и
, и 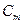 ).
).
Между указанными теплоемкостями существует функциональная связь
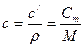 . (1. 12)
. (1. 12)
Объемную теплоемкость газа принято относить к объему при нормальных условиях. Поэтому при ее расчете используют плотность газа при нормальных условиях.
Теплоемкость газа зависит от характера процесса подвода (отвода) теплоты, от природы газа, его температуры и давления.
Особое значение в тепловых расчетах имеют теплоемкости газа в процессах при постоянном давлении и постоянном объеме – соответственно изобарная и изохорная теплоемкости. Их связывает между собой уравнение Майера:
– для 1 кг газа
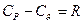 , (1. 13)
, (1. 13)
где 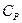 и
и 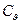 – изобарная и изохорная удельные теплоемкости;
– изобарная и изохорная удельные теплоемкости;
– для 1-го моля газа
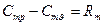 , (1. 13а)
, (1. 13а)
где 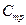 и
и 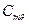 – изобарная и изохорная молярные теплоемкости.
– изобарная и изохорная молярные теплоемкости.
Отношение этих теплоемкостей называют показателем адиабаты
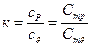 . (1. 14)
. (1. 14)
Для приближенных расчетов при невысоких температурах можно принимать постоянные значения молярных теплоемкостей и показателей адиабаты (приложение В). В этом случае считают теплоемкость газа постоянной.
С учетом зависимости теплоемкости от температуры различают истинные и средние теплоемкости. Истинную теплоемкость определяют при малом (бесконечно малом) изменении температуры, а среднюю – при конечном (заданном) интервале температур.
Среднюю теплоемкость в интервале температур от 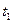 до
до 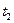 принято рассчитывать как
принято рассчитывать как

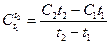 , (1. 15)
, (1. 15)
где 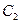 и
и 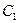 – средние теплоемкости в интервалах температур от 0 до
– средние теплоемкости в интервалах температур от 0 до 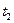 0С и от 0 до
0С и от 0 до 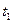 0С.
0С.
Значение средних изобарных теплоемкостей некоторых газов приведены в приложении Г.
Теплоемкости смеси газов:
– удельная
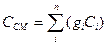 , (1. 16)
, (1. 16)
где 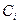 – удельная теплоемкость компонента;
– удельная теплоемкость компонента;
– объемная
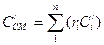 , (1. 16а)
, (1. 16а)
где 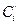 – объемная теплоемкость компонента;
– объемная теплоемкость компонента;
– молярная
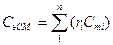 , (1. 16б)
, (1. 16б)
где 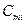 – молярная теплоемкость компонента.
– молярная теплоемкость компонента.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|