Контакты

Случайная статья

Формула Тейлора для функций двух переменных

⇐ ПредыдущаяСтр 2 из 2

Если функция 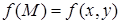имеет в некоторой окрестности точки 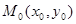непрерывные частные производные до ( 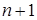) -го порядка включительно, то в этой окрестности справедлива формула

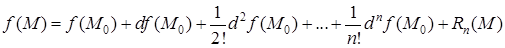
Здесь 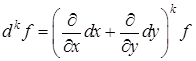берется в точке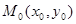

Остаточный член в форме Лагранжа имеет вид

,

, , , .

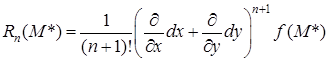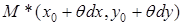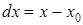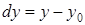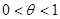Остаточный член в форме Пеано (при более слабых предположениях).

, .

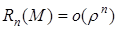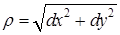Пример 4. Для функции 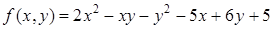записать формулу Тейлора в окрестности точки .

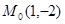Решение. Подсчитаем 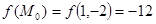. Найдем частные производные первого порядка:

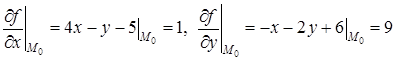
Запишем первый дифференциал в точке :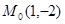

.

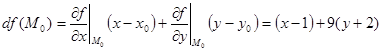Найдем вторые производные:

, , .

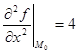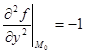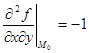Запишем второй дифференциал в точке :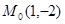

.

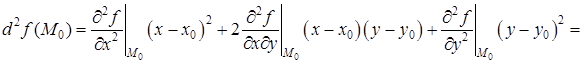
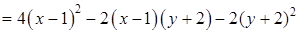Все производные порядка выше второго равны нулю. Формула Тейлора принимает вид

.

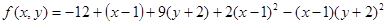Фактически мы перегруппировали данный многочлен по степеням 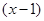и . ☻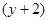

Пример 5. Записать формулу Тейлора 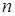-го порядка для функции 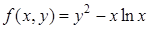в окрестности точки .

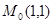Решение. Находим 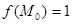. Подсчитаем частные производные первого порядка

.

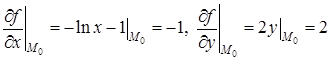Запишем первый дифференциал в точке :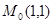

.

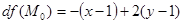Подсчитаем вторые производные:

, , .

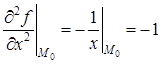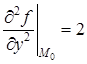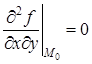Запишем второй дифференциал в точке :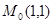

.

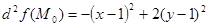Продолжаем дифференцировать: 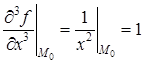, все остальные производные 3-го порядка равны нулю.

Запишем третий дифференциал в точке : .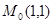

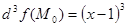Легко заметить, что дальнейшее дифференцирование по 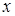приводит к формуле 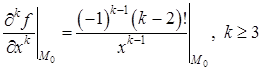. Значит,

, .

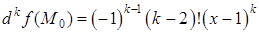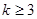Формула Тейлора принимает вид:

,

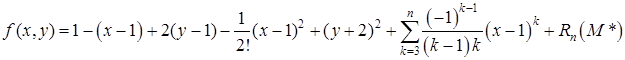где , . ☻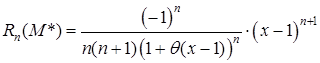

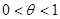В частном случае при 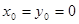получаем формулу Маклорена.

Пример 6. Функцию 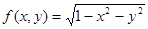разложить по формуле Маклорена до членов второго порядка функцию .

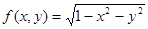Решение. Находим 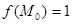. Чтобы записать первый дифференциал, находим

.

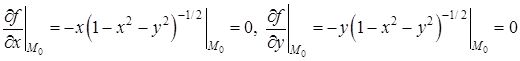Так как 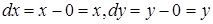, то .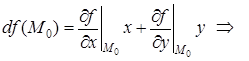

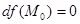Чтобы записать второй дифференциал, находим

.

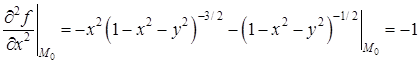
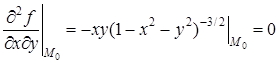
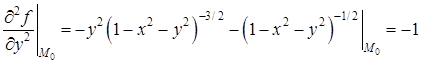Так как 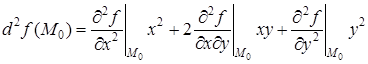, то .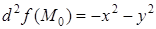

Формула Маклорена принимает вид

, . ☻

⇐ Предыдущая 12

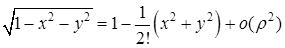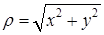© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.