
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
2. Оценка фазы без шума. 3. Оценка фазы с шумом
2. Оценка фазы без шума
1. Установим произвольную фазу с помощью виртуального контроллера «Фаза Ф2». Построим сигнальную функцию, не изменяя фазу Ф2 (Рис. 5). По максимуму сигнальной функции оценим неизвестную фазу Ф2 ≈ 85°.
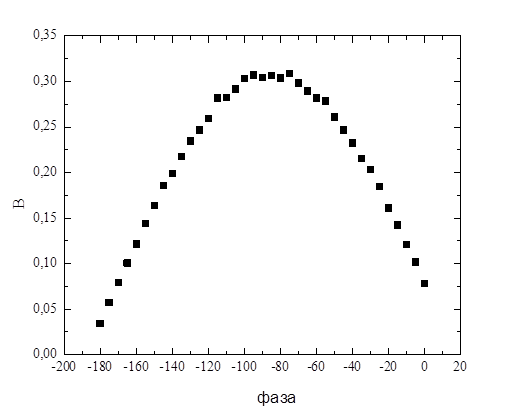
Рисунок 5 – Сигнальная функция для неизвестной фазы Ф2
3. Оценка фазы с шумом
1. Соберем модули согласно схеме (Рис. 6). Полученной схеме соответствует блок-схема (Рис. 7).
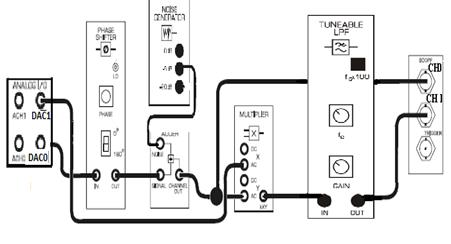
Рисунок 6 – Соединение проводников для оценки фазы с шумом
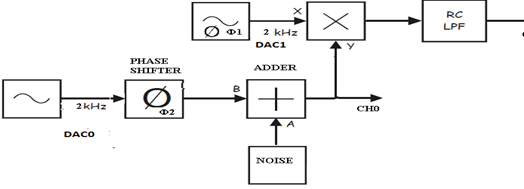
Рисунок 7 – Блок-схема установки
2. Проверить, что виртуальный контроллер «Фаза 2» установлен с положение, которое было в пункте 2.
3. Оценим нижнюю границу дисперсии 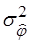 оцениваемой фазы (не учитываем m)
оцениваемой фазы (не учитываем m)
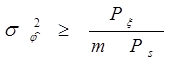 (рад2)
(рад2)
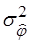 = 2. 4В/1В = 2. 4 рад2 => σ = 89°
= 2. 4В/1В = 2. 4 рад2 => σ = 89°
4. Варьируя фазу Ф1 в интервале 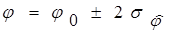 от -135° до -35° с шагом 5°. Повтором измерения m=6 раз. Построим сигнальную функцию для каждого измерения (Рис. 8).
от -135° до -35° с шагом 5°. Повтором измерения m=6 раз. Построим сигнальную функцию для каждого измерения (Рис. 8).
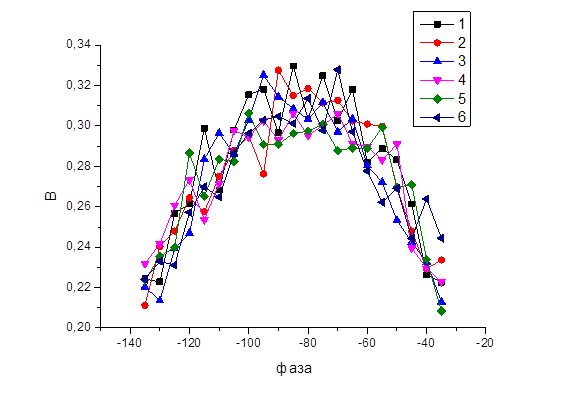
Рисунок 8 – Функция взаимной корреляции для m=6 измерений
5. Проведем статистическую обработку результатов измерений фазы. Вычислим среднее значение оценки фазы и дисперсию оценки фазы по формулам:
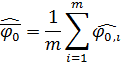
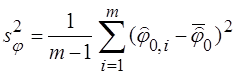
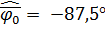
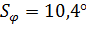
6. Вычислим теоретическую нижнюю границу оценки фазы 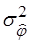 по формуле:
по формуле:
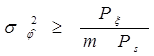 =
= 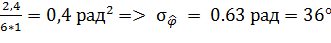
7. Введем коэффициент для учета того, что рассматриваемый нами диапазон отличается от рассчитанного, т. к. оценка искалась в более узком диапазоне значений.
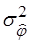 = 2. 4В/1В = 2. 4 рад2 =>
= 2. 4В/1В = 2. 4 рад2 => 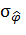 = 89°, где m=1
= 89°, где m=1
Учитывая, что диапазон, в котором изменялся параметр = 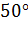
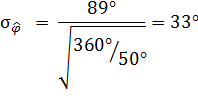
8. Сравним теоретическую и экспериментальную дисперсию 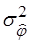 и
и 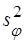
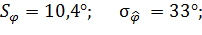
9. На оси (0, φ ) отложим точки
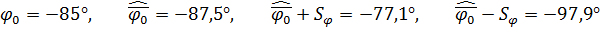

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|