
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант 2. 2.Решение задач.
Вариант 2
1. Стереометрия – это раздел геометрии, в котором изучаются свойства:
а) прямых в пространстве; б) фигур в пространстве; в) фигур на плоскости;
г) плоскостей в пространстве.
2. Какие три из изображенных фигур не являются основными в пространстве?

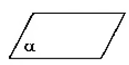
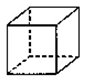
а) треугольник
б) отрезок
в) плоскость
г) куб
3. Перепишите утверждения, вставьте пропущенные слова в утверждениях:
«Через любые ___ точки, не лежащие на одной ________, проходит ______, и притом только одна. Если ____ точки прямой лежат в ____, то все точки _________ лежат в этой _____. Если две _______ имеют общую точку, то они имеют общую ______, на которой лежат все общие точки этих ________. »
4. Какое наименьшее число точек определяет прямую в пространстве?
а) одна точка; б) две точки; в) три точки; г) четыре точки.
5. Сколько плоскостей можно провести через прямую в пространстве?
а) одну; б) две; в) три; г) бесконечно много.
6. Что называют теоремой в геометрии?
7. Сколько аксиом в планиметрии в Евклидовой геометрии?
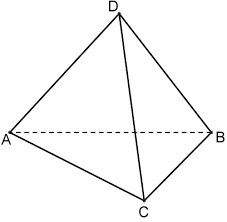
8. Изобразите тетраэдр. Пользуясь рисунком, назовите:
а) точку, не принадлежащую плоскости (BCD)
б) прямую, по которой пересекаются плоскости (BCD) и (ABС)
в) плоскость, проходящую через прямые AС и CD
2. Решение задач.
 Задание №1
Задание №1
 Решение:
Решение:
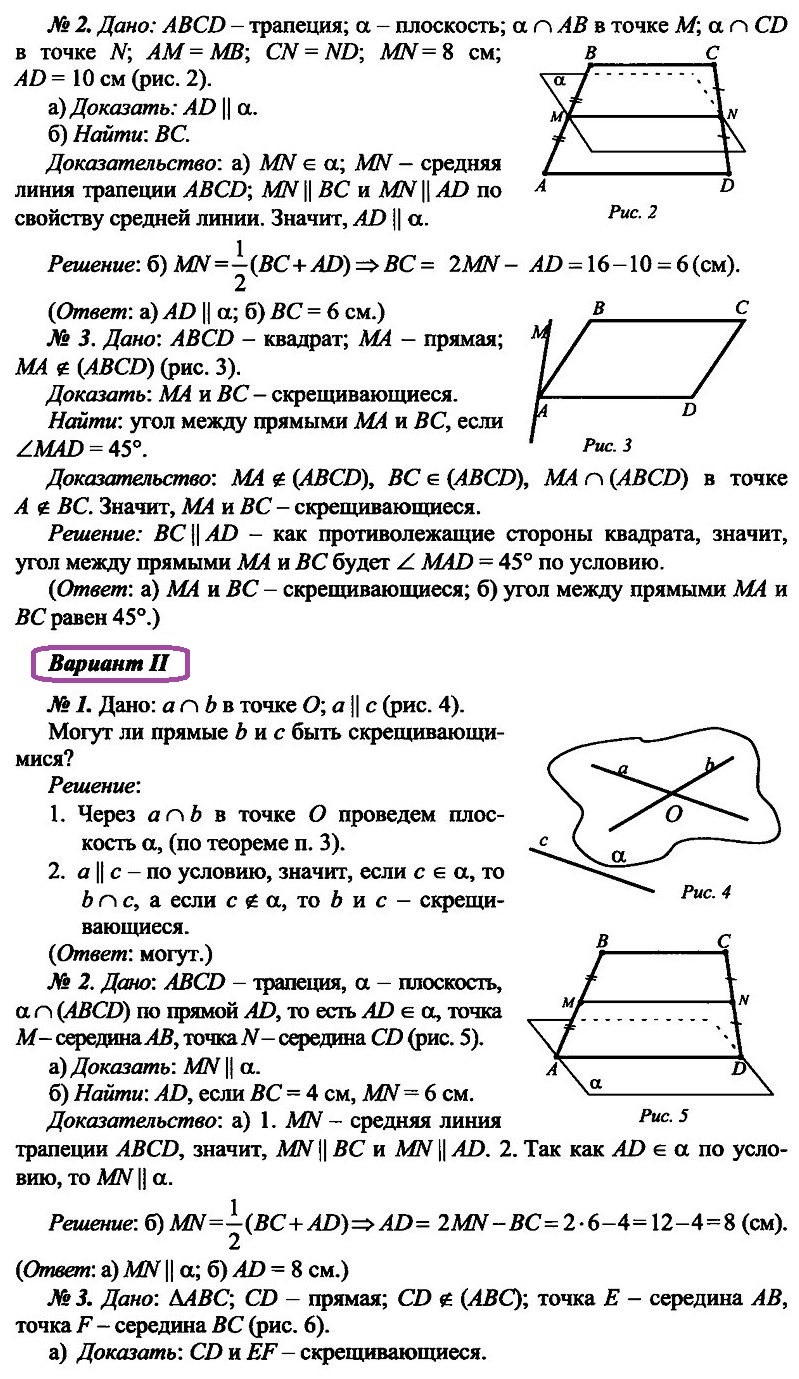
 Задание №2 Плоскости α и β пересекаются по прямой l. Прямые l и а пересекаются, а прямые l и b параллельны. Определите, могут ли прямые а и b: а) лежать в одной из плоскостей; б) лежать в разных плоскостях α и β; в) пересекать плоскости α и β. В случае утвердительного ответа укажите взаимное расположение прямых а и b.
Задание №2 Плоскости α и β пересекаются по прямой l. Прямые l и а пересекаются, а прямые l и b параллельны. Определите, могут ли прямые а и b: а) лежать в одной из плоскостей; б) лежать в разных плоскостях α и β; в) пересекать плоскости α и β. В случае утвердительного ответа укажите взаимное расположение прямых а и b.
 Задача №3 Точка М не лежит в плоскости трапеции ABCD (AD II ВС). а) Докажите, что треугольники MAD и МВС имеют параллельные средние линии; б) Найдите длины этих средних линий, если AD: ВС = 5: 3, а средняя линия трапеции равна 16 см.
Задача №3 Точка М не лежит в плоскости трапеции ABCD (AD II ВС). а) Докажите, что треугольники MAD и МВС имеют параллельные средние линии; б) Найдите длины этих средних линий, если AD: ВС = 5: 3, а средняя линия трапеции равна 16 см.
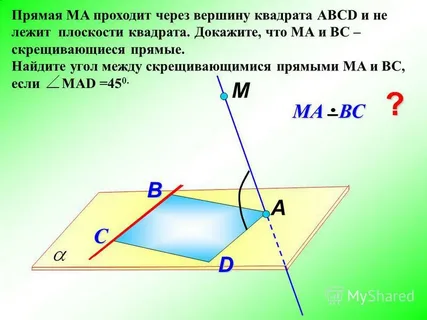
 Задача №4 Через вершину А квадрата ABCD проведена прямая КА, не лежащая в плоскости квадрата. a) Докажите, что КА и CD — скрещивающиеся прямые. б) Найдите угол между КА и CD, если ∠ АКВ = 85°, ∠ АВК = 45°.
Задача №4 Через вершину А квадрата ABCD проведена прямая КА, не лежащая в плоскости квадрата. a) Докажите, что КА и CD — скрещивающиеся прямые. б) Найдите угол между КА и CD, если ∠ АКВ = 85°, ∠ АВК = 45°.
Задание №5 Точки А, В, С и D не лежат в одной плоскости. Найдите угол между прямыми АС и ВД, если АС = 6 см, BD = 8 см, а расстояние между серединами отрезков AD и ВС равно 5 см.
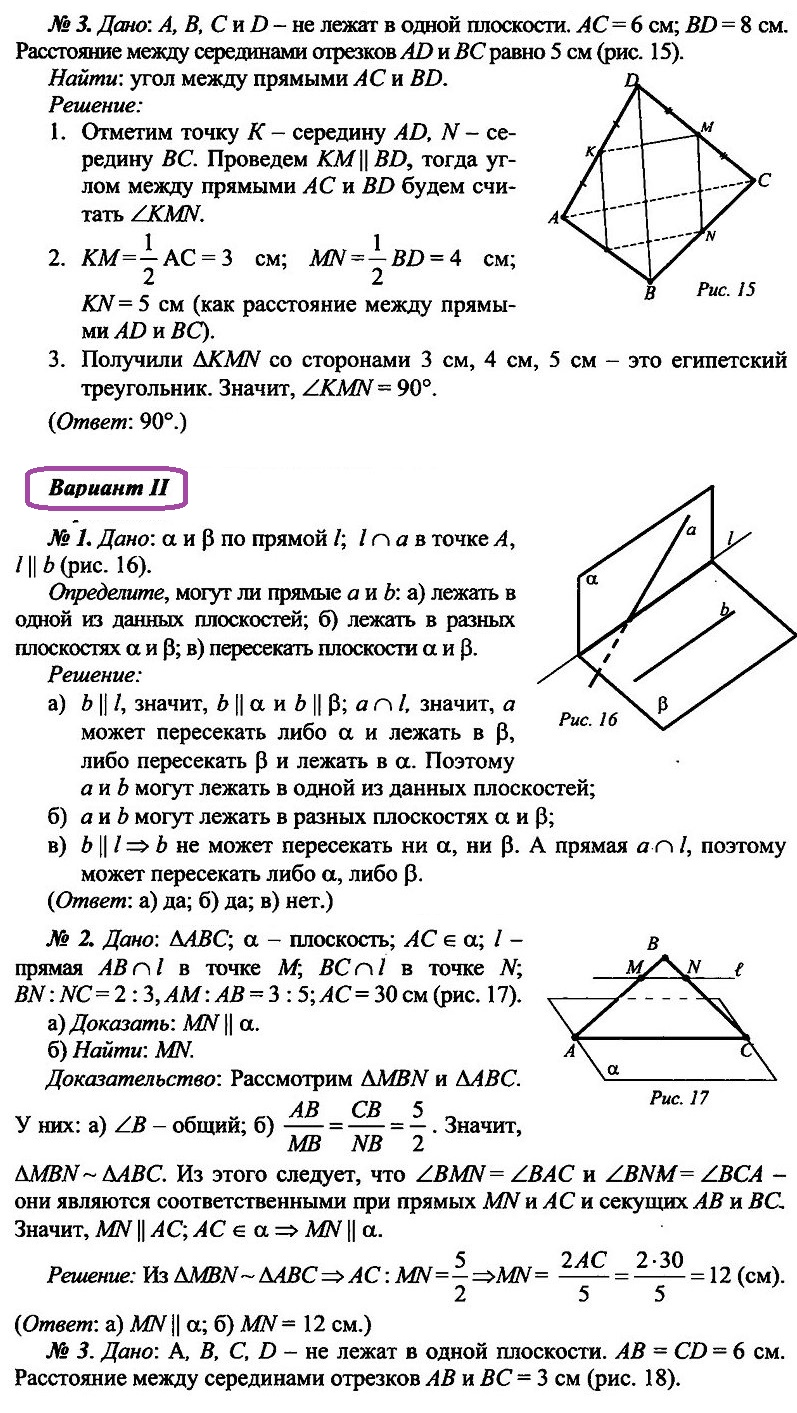 Решение:
Решение:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|