Критические значения χ2 при разных степенях свободы для уровней значимости p=0,05 и р=0,01 (по Фишеру)

Критерий χ ² Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Иначе, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей.

Для того, чтобы вычислить величину χ ² для конкретного случая необходимо воспользоваться формулой:

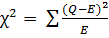где Q – наблюдаемая величина (эмпирическая), E – ожидаемая величина (теоретическая).

Чем выше значение χ ², тем серьезнее расхождение. При превышении критического значения (приведены ниже) связь между теоретическим распределением и практически наблюдаемым будет отвергнута.

В биологической статистике при непосредственной оценке значимости тех или иных экспериментальных данных используются понятия – уровень значимости и число степеней свободы.

Каждый раз, когда мы утверждаем достоверность тех или иных выявленных закономерностях, мы не можем быть уверенными в их абсолютной верности и точности. Всегда есть вероятность того, что мы выдвинули ложную гипотезу, и она подтвердилась ввиду случайных событий. Однако, мы можем численно оценить вероятность этой случайности. Под уровнем значимости р подразумевают вероятность отклонить гипотезу, в случае если она верна. Общепринятыми уровнями значимости являются p=0, 05 и р=0, 01. Критические значения χ ² будут различны для разных уровней значимости.

Число степеней свободы. Из формулы χ ² видно, что это сумма неотрицательных величин. Соответственно, она будет тем больше, чем большее количество элементов мы складываем. Отсюда очевидна необходимость различных критических значений χ ², в зависимости от того, какое количество категорий объектов участвует в сравнении. Для учета этого параметра вводится понятие числа степеней свободы. Число степеней свободы k на единицу меньше полученных в эксперименте групп особей (n-1, так как последний класс может быть подсчитан вычитанием суммы всех остальных классов из общего числа).

Если же мы отслеживаем сопряженные признаки, например, пол и цвет глаз (особь не может иметь только красные глаза или быть только самцом), то в таком случае число степеней свободы расcчитывается по формуле k = (r – 1) × (c – 1), где r и c количество фенотипических классов в каждом из отслеживемых параметров.

Критические значения χ 2 при разных степенях свободы для уровней значимости p=0, 05 и р=0, 01 (по Фишеру)

Число степеней свободы	Уровень значимости
Число степеней свободы	0, 05	0, 01
	3, 841	6, 635
	5, 991	9, 210
	7, 815	11, 341
	9, 488	13, 277
	11, 070	15, 086
	12, 592	16, 812
	14, 067	18, 475

Используя метод χ ², следует помнить:

· результат проверки не подтверждает гипотезу, а показывает, что нет достаточных оснований для ее отклонения;

· дает хорошие результаты в случае, когда мы имеем дело с большой выборкой и достаточной численностью каждого класса.

В случае одной степени свободы, численность каждого из классов не должна быть менее 5. В случае количества степеней свободы, превышающего единицу – число особей внутри каждого класса не должно быть меньше одного.

12 Следующая ⇒