Задача 2.. Задача 3.

Задача 2.

а) Найдите точку пересечения прямой DК с плоскостью АВС.

Решение:

Прямая DК содержит точку С. Плоскость АВС содержит точку С. Значит, прямая DК и плоскость АВС пересекаются в точке С.

б) Найдите точку пересечения прямой СЕ с плоскостью АDВ.

Решение:

Точка Е принадлежит и прямой СЕ, и плоскости АDВ. Значит, Прямая СЕ пересекается с плоскостью АDВ в точке Е.

Задача 3.

а) Найдите точки, лежащие одновременно в плоскостях АDВ и DВС.

Решение:

Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит, 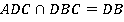. Все точки прямой DВ являются ответом.

б) Найдите прямые, по которым пересекаются плоскость АDВ и DВС.

Решение:

Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит, прямая DВ есть прямая, по которой пересекаются заданные плоскости.

в) Назовите прямые, по которым пересекаются плоскости АDВ и СDА.

Решение:

Точки А, D лежат в плоскости АDВ, а также точки А, D лежат в другой плоскости СDА. Значит, АD – линия их пересечения: .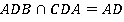

г) Назовите прямые, по которым пересекаются плоскости РDС и АВС.

Решение:

Плоскость РDС совпадает с плоскостью ЕDС. Точка Е и точка С одновременно лежат в двух плоскостях: РDС и АВС. Значит, СЕ – это линия пересечения двух плоскостей.

⇐ Предыдущая 1 2 345 6 Следующая ⇒