Математическая олимпиада школьников

Математическая олимпиада школьников

имени Г. П. Кукина

г. Снежинск, 06. 02. 22, 6 класс

Математическая олимпиада ОмГУ носит имя профессора Г. П. Кукина, создателя системы городских математических олимпиад.

Выводные задачи

7. В полдень из разных мест стартовали два гонца. Они движутся по одной прямой дороге, каждый со своей постоянной скоростью. В 1 час дня между ними было расстояние 1 верста, в 2 часа - 4 версты, в 3 часа - 9 вёрст. Найдите расстояние между местами старта.

8. На праздник каждый должен был прийти с одним воздушным шаром, рыцари выбрали красный цвет, лжецы – синий, а хитрецы – желтый. В финале праздника все выпустили веревочки, и небо украсили 30 шаров всех трех цветов!

20 человек воскликнули: «Синих шаров больше всех! »

7 других человек прокричали: «Красных шаров больше всех! »

А еще 3 человека кричать не стали, но произнесли: «Желтых и синих шаров поровну». Сколько красных шаров было в небе?

Рыцари говорят только правду, лжецы всегда лгут, а хитрецы могут говорить как ложь, так и правду.

9. Кубики расположили, так как показано на рисунке. Если читать то, что написано, выйдет «Кантор», а если перевернуть башню вверх ногами – получится «картон». Какое наименьшее количество типов кубиков понадобится для такой сборки? Один тип кубиков может отличаться от другого как набором букв на гранях, так и взаимным расположением букв.

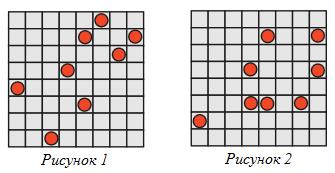
10. Женя и Саша играют в игру с фишками на клетчатой доске 8× 8. В свой ход каждый может сделать одно из действий: передвинуть выбранную фишку по диагонали, или же любые две фишки, являющиеся вершинами прямоугольника со сторонами параллельными сторонам доски, можно переместить в две другие вершины этого прямоугольника (если это возможно). Во время игры Саше пришлось отойти, а когда он вернулся, то увидел на доске следующую позицию (рис 1. ). Саша не помнит предыдущие позиции, однако начальная у него записана (рис 2. ). Он уверен, что Женя сжульничал. Прав ли Саша?

⇐ Предыдущая 12