Хелпикс

Главная

Контакты

Случайная статья



Примеры.. Вопросы для самопроверки

⇐ ПредыдущаяСтр 2 из 2


Примеры.

1. Найти производную функции y = x2

а) в произвольной точке;

б) в точке x= 2.

а)

1. f(x + Δ x) = (x + Δ x)2;

2. Δ y = (x + Δ x)2 – x2=2xΔ x– x2;

3. .

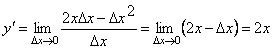б) f '(2) = 4

2. Используя определение найти производную функции 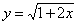 в произвольной точке.

1. .

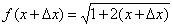2.  

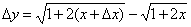
3.

 

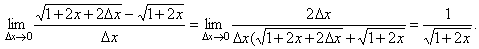
Учитывая задачи о мгновенной скорости и касательной к графику легко построить следующие утверждения:

Физический смысл производной: скорость неравномерного движения это производная от пройденного пути по времени.

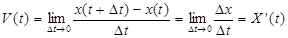
Геометрический смысл производной: у'(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0 (т. е. при данном значении аргумента x, производная равна тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке М0(x; y) с положительным направлением оси Ox).

Определение. Касательной к графику функции в точке М0(x0, y0) назовем предельное положение секущей М0М, когда точка М, двигаясь вдоль кривой, стремиться к совпадению с точкой М0. .

Уравнение касательной к графику функции в точке М0 (x0, y0):

.

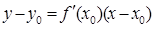(вывод формулы самостоятельно, у=kx+b-уравнение прямой, k= )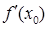

3. Производная суммы/разности

Итак, мы дали определение производной, объяснили ее физический и геометрический смысл. Теперь необходимо сделать следующий шаг - рассмотреть правила дифференцирования.

Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x), v=v(x) – две дифференцируемые функции от переменной x.

Основные правила дифференцирования выражаются формулами:

1.

·

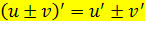
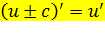
2.

·

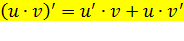
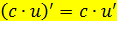
3.

·

·

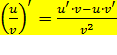
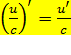
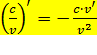
Доказательство формулы 1.

Пусть y = u(x) + v(x). Для значения аргумента x+Δ x имеем y(x+Δ x)=u(x+Δ x) + v(x+Δ x).

Тогда

Δ y=y(x+Δ x) – y(x) = u(x+Δ x) + v(x+Δ x) – u(x) – v(x) = Δ u +Δ v.

Следовательно,

.

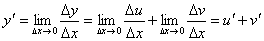(построить вывод следствия)

4. Производная произведения/частного

Доказательство формулы 2.

Пусть y=u(x)·v(x). Тогда y(x+Δ x)=u(x+Δ x)·v(x+Δ x), поэтому

Δ y=u(x+Δ x)·v(x+Δ x) – u(x)·v(x).

Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δ x)→ u(x), v(x+Δ x)→ v(x), при Δ x→ 0.

Поэтому можем записать

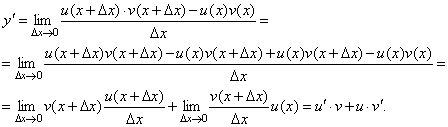
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций.

Пусть, например, y=u·v·w. Тогда,

y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '.

(построить вывод следствия)

Доказательство формулы 3.

Пусть 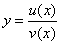. Тогда

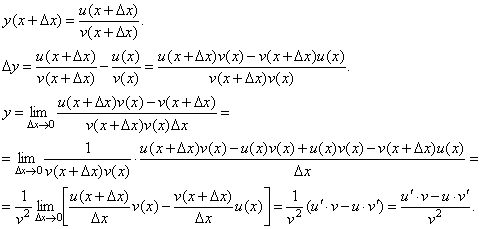
При доказательстве воспользовались тем, что v(x+Δ x)→ v(x) при Δ x→ 0.

(построить вывод следствий)

 

Вопросы для самопроверки

1) При каком движении средняя скорость всегда совпадает с мгновенной?

2) Закон прямолинейного движения тела выражается формулой x = kt + b. Какое механическое содержание коэффициентов k, b?

3) Дать определения производной заданной функции.

4) Охарактеризовать символы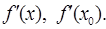

5) Который геометрический и физический смысл производной?

6) Как найти производную, исходя из ее определения?

7) Доказать, пользуясь определением производной,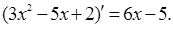


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.