Тема. Понятие о производной функции, ее геометрический и физический смысл. Производная суммы, разности, произведения, частного.

Перейдем к основным идеям одного из важнее разделов математики – дифференциального исчисления. Методы дифференциального исчисления дают возможность свести изучение сложного процесса к более простому – равномерному, найти его скорость и ускорение, определить условия оптимального прохождения процесса, оценить допущенные погрешности, построить графики и др. Дифференциальное исчисление – раздел математики, в котором рассматривается исследования функций с помощью производных и дифференциалов.

1. Задачи, которые приводят к понятию производной

Задача 1 (о мгновенной скорости). Пусть некоторая материальная точка движется по оси x, так что x(t) есть координата точки в момент времени t. Спустя время 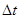координата точки будет 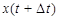, т. е. за время 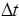точка пройдет путь 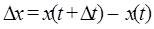. Поэтому средняя скорость точки за интервал времени 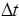будет равна 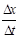. Чтобы найти мгновенную скорость точки в момент времени 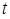надо устремить 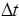к нулю, то есть

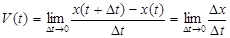
Задача 2 (о касательной к графику). Пусть кривая задана уравнением 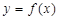. Соединим две ее точки М₀( 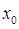, 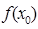) и М( 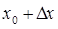, 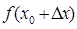) секущей.

Тогда дробь 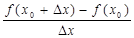= 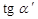, где 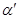есть угол наклона секущей к оси OX (в треугольнике М₀МТ отношение катетов)

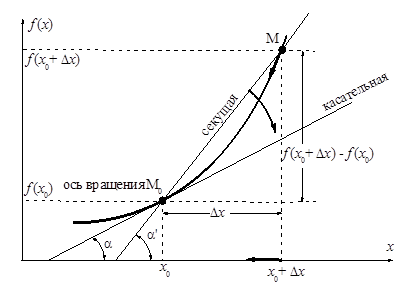
При 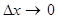точка M начинает двигаться к точке M₀. При этом вся секущая будет поворачиваться около точки M₀ и в пределе она превратиться в касательную к точке M₀. Угол 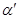при этом перейдет в угол 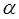, который эта касательная образует с осью х. Поэтому можно утверждать, что

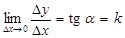где 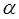- угол, образованный касательной к кривой в точке 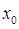и осью OX, k - угловой коэффициент касательной.

Задача 3 (о скорости химической реакции) Пусть g(t) есть количество вещества прореагировавшего за время t. Спустя время 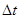количество прореагировавшего вещества будет 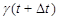, т. е. за время 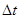количество прореагировавшего вещества 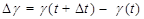. Поэтому средняя скорость химической реакции за интервал времени 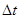будет равна 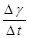. Чтобы найти мгновенную скорость химической реакции в момент времени 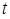надо устремить 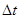к нулю, то есть

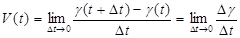
Поскольку с помощью предела 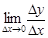решают кроме рассмотренных ещё и много других важнейших задач (например: задача о величине переменного тока, который течет в проводнике; нахождении линейной плотности неоднородного стержня, теплоемкости тела при его нагревании, угловой скорости тела, которое вращается и многие др), то целесообразно всесторонне изучить данный предел, в частности, указать способы его вычисления. Этот предел в математике и носит название производной.

2. Производная, ее геометрический и физический смысл

Определение: Производной данной функции y=f(x) называется предел отношения приращения функции Δ y к приращению аргумента Δ x, когда последнее стремится к нулю и такой предел существует и конечен.

Заметим, что производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x)

Производная обозначается символами f'(x), y', 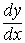. Конкретное значение производной при x=a обозначается f'(a) или y'|_x=a.

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило:

1. Придать x приращение Δ x и найти наращенное значение функции f(x + Δ x).

2. Найти приращение функции Δ y = f(x + Δ x) – f(x).

3. Составить отношение 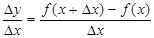и найти предел этого отношения при Δ x→ 0.

12 Следующая ⇒