Хелпикс

Главная

Контакты

Случайная статья



Номер варианта выбирается из таблицы по шестой цифре номера зачётной книжки. Например, зачётная книжка № 931417 ® Вариант № 7.

⇐ ПредыдущаяСтр 3 из 3


Задание № 9.

1. Добавить новый лист. Переименовать его в “Прогрессия” и поместить в конец.

2. Заполнить в столбик последовательность первых 20 членов прогрессии, найти их сумму и произведение. Для этого сначала заполнить столбец номеров 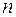 членов прогрессии, используя автозаполнение числами, затем столбец членов прогрессии 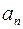, используя автозаполнение формулой (В условии заданы несколько первых элементов прогрессии – 1й, 2й и 3й в зависимости от варианта. Все остальные элементы вычисляются по рекуррентной формуле, т. е. через известные предыдущие элементы прогрессии. ) и столбцы суммы  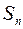и произведения  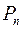всех членов прогрессии, расположенных выше данной строки. Сумму и произведение элементов прогрессии также вычисляют по рекуррентной формуле:

; ;

.

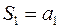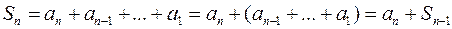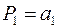
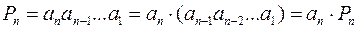Номер варианта выбирается из таблицы по шестой цифре номера зачётной книжки. Например, зачётная книжка № 931417 ® Вариант № 7.

Варианты задания.

№ Первый член прогрессии 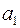Второй член прогрессии 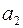Третий член прогрессии 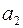Рекуррентная формула
– 0, 8 3, 15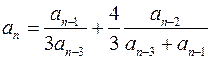
0, 3 –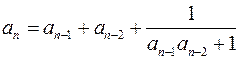
1, 5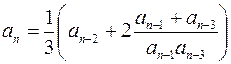
0, 7 – 1 –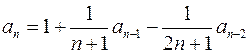
–
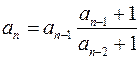
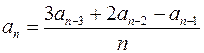
– 1 0, 2 1, 2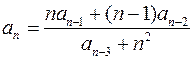
– –
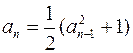
1, 3 1, 8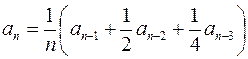

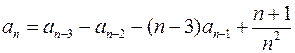
3. Проверить правильность накопления суммы членов прогрессии, используя автосумму.

4. Подробно, по пунктам, описать все свои действия в пояснительной записке.

 

Задание № 10.

1. Добавить новый лист. Переименовать его в “Поверхность” и поместить в конец.

2. В строку (начиная с ячейки В1) введите последовательность значений X на отрезке [a; b] c шагом h.

3. В столбец (начиная с ячейки А2) введите последовательность значений Y на отрезке [a; b] c шагом h.

4.  В ячейке B2 введите зависимость Z(x, y), и используя автозаполнение получите матрицу значений Z(x, y) на диапазоне [a; b].

5. Используя данные п. 1-4 постройте поверхность Z(x, y).

6. Подробно, по пунктам, описать все свои действия в пояснительной
записке.

 

№ Отрезок Шаг Уравнение поверхности
[-2; 2] 0, 4 x2 /4+y2 /3 – z2 =0
[-1; 1] 0, 2 x2 +y2 z2 /2=0
[-2; 2] 0, 4 x2 /2+y2 – z =0
[-1; 1] 0, 2 x2 /2 + y2 /4 – 3z =0
[-2; 2] 0, 4 2xy-z =0
[-1; 1] 0, 2 0, 5 xy-3z =0
[-2; 2] 0, 4 x2 /2+y2 /4 – z =0
[-1; 1] 0, 2 x2 -y2 – 2z =0
[-2; 2] 0, 4 x2 +y2 + z2 =0
[-1; 1] 0, 2 2x2 +3y2 – 4z2 =0

 

 


⇐ Предыдущая123
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.