
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Площадь поверхности правильной четырехугольной призмы выражается через сторону ее основания и боковое ребро как. Вариант-2. по теореме Пифагора. Тогда длина ребра равна
Решение.
Площадь поверхности правильной четырехугольной призмы выражается через сторону ее основания и боковое ребро как
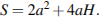
Подставим значения  и
и 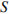 :
:
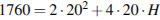 ,
,
откуда находим, что 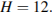
Ответ: 12.
Ответ: 12
Вариант-2
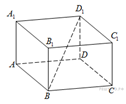 1. В прямоугольном параллелепипеде
1. В прямоугольном параллелепипеде 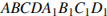 известно, что
известно, что 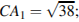
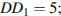
 Найдите длину ребра
Найдите длину ребра 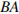 .
.
 Решение.
Решение.
по теореме Пифагора
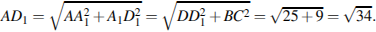
Тогда длина ребра равна
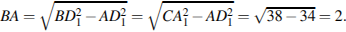
Ответ: 2.
Ответ: 2
2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 180 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 6 раз больше, чем у первого? Ответ выразите в сантиметрах.
 3. В основании прямой призмы лежит ромб с диагоналями, равными 16 и 30. Площадь ее поверхности равна 2588. Найдите боковое ребро этой призмы.
3. В основании прямой призмы лежит ромб с диагоналями, равными 16 и 30. Площадь ее поверхности равна 2588. Найдите боковое ребро этой призмы.
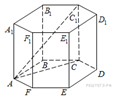
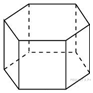
 4. Найдите объем многогранника, вершинами которого являются точки
4. Найдите объем многогранника, вершинами которого являются точки 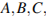
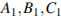 правильной шестиугольной призмы
правильной шестиугольной призмы 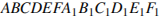 , площадь основания которой равна 6, а боковое ребро равно 3.
, площадь основания которой равна 6, а боковое ребро равно 3.
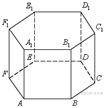
 5. В правильной шестиугольной призме
5. В правильной шестиугольной призме 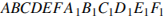 все ребра равны 1. Найдите угол
все ребра равны 1. Найдите угол 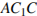 . Ответ дайте в градусах.
. Ответ дайте в градусах.
6. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны 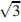 .
.
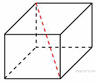 7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. Решение.
7. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ. Решение.
Обозначим известные ребра за  и
и 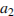 , а неизвестное за
, а неизвестное за 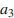 . Площадь поверхности параллелепипеда выражается как
. Площадь поверхности параллелепипеда выражается как 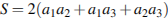 . Выразим
. Выразим 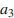 :
:
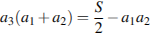 ,
,
откуда неизвестное ребро
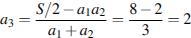 ,
,
Диагональ параллелепипеда находится как
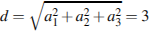 .
.
Ответ: 3.
Ответ: 3
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|