
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Производные некоторых элементарных функций
Производные некоторых элементарных функций
1. 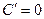 9.
9. 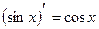
2. 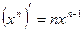 10.
10. 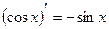
3. 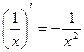 11.
11. 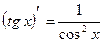
4. 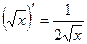 12.
12. 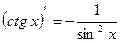
5. 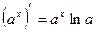 13.
13. 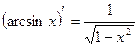
6. 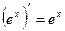 14.
14. 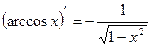
7. 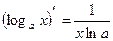 15.
15. 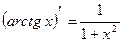
8. 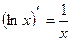 16.
16. 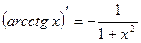
Производная сложной функции
Пусть задана сложная функция 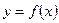 , т. е. такая, что её можно представить в виде:
, т. е. такая, что её можно представить в виде:
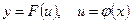
или 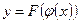 . В выражении
. В выражении 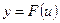 переменная u называется промежуточным аргументом.
переменная u называется промежуточным аргументом.
Теорема. Если функция 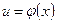 имеет в некоторой точке x производную
имеет в некоторой точке x производную 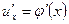 , а функция
, а функция 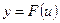 имеет при соответствующем значении u производную
имеет при соответствующем значении u производную 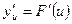 , то сложная функция
, то сложная функция 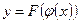 в указанной точке x также имеет производную, которая равна
в указанной точке x также имеет производную, которая равна
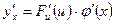 ,
,
где вместо u должно быть подставлено выражение 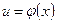 .
.
Коротко,
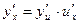 ,
,
т. е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.
Пример: Дана функция 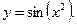 . Найдите
. Найдите 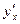 .
.
Решение. Введем промежуточный аргумент u:
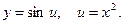
Тогда 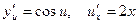 . По правилу дифференцирования сложной функции получаем:
. По правилу дифференцирования сложной функции получаем:
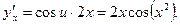
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|