
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Определение производной. Производная суммы, разности, произведения и частного функций
Определение производной
Определение производной. Пусть задана функция 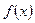 ,
, 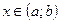 и пусть
и пусть 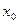 - некоторая точка интервала
- некоторая точка интервала 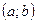 . Предел
. Предел
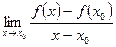
называется производной функции 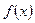 в точке
в точке 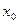 и обозначается
и обозначается 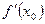 (если последний предел существует). Таким образом, по определению,
(если последний предел существует). Таким образом, по определению,
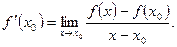
Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке. Функция 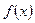 ,
, 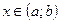 , имеющая в каждой точке интервала
, имеющая в каждой точке интервала 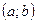 производную, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием.
производную, называется дифференцируемой на этом интервале. Операция нахождения производной данной функции называется дифференцированием.
Обозначение производной функции 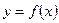 :
: 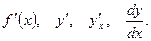
Если ввести приращение аргумента 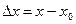 и приращение функции
и приращение функции 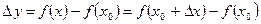 , определение производной запишется в виде
, определение производной запишется в виде
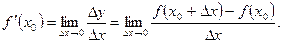
Производная суммы, разности, произведения и частного функций
Теорема 1. Если функции 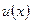 и
и 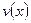 дифференцируемы на некотором интервале, то на этом интервале
дифференцируемы на некотором интервале, то на этом интервале
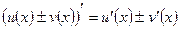
т. е. производная суммы (разности) функций равна сумме (разности) производных этих функций.
Теорема 2. Если функции 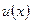 и
и 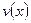 дифференцируемы на некотором интервале, то на этом интервале
дифференцируемы на некотором интервале, то на этом интервале
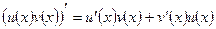 .
.
Следствие. Постоянный множитель можно выносить за знак производной, т. е. 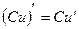 , где
, где 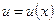 - дифференцируемая функция.
- дифференцируемая функция.
Теорема 3. Если функции 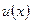 и
и 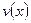 дифференцируемы на некотором интервале и
дифференцируемы на некотором интервале и 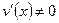 для любого x из этого интервала, то
для любого x из этого интервала, то
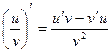 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|