Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство

Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство

В - Р + Г = 2,

где В - число вершин, Р - число ребер и Г - число граней данного многогранника.

Заметим, что многоугольники можно деформировать, увеличивать, уменьшать или даже искривлять их стороны, лишь бы при этом не происходило разрывов сторон. Число вершин, ребер и граней при этом не изменится.

Свойство 4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.

Самостоятельная работа

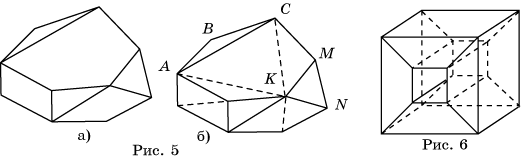
1. На рисунке 1 укажите выпуклые и невыпуклые многогранники.

2. Приведите пример невыпуклого многогранника, у которого все грани являются выпуклыми многоугольниками.

3. Верно ли, что объединение выпуклых многогранников является выпуклым многогранником?

4. Может ли число вершин многогранника равняться числу его граней?

5. Установите связь между числом плоских углов П многогранника и числом его ребер Р.

6. Из каждой вершины выпуклого многогранника выходит три ребра. Сколько он имеет вершин В и граней Г, если у него: а) 12 ребер; б) 15 ребер? Нарисуйте эти многогранники.

7. В каждой вершине выпуклого многогранника сходится по четыре ребра. Сколько он имеет вершин В и граней Г, если число ребер равно 12? Нарисуйте эти многогранники.

8. Чему равно В – Р + Г для многогранника, изображенного на рисунке 6?

⇐ Предыдущая 123 Следующая ⇒