Тема: Понятие многогранника. Теорема Эйлера.

Тема: Понятие многогранника. Теорема Эйлера.

Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л. С., глава III, § 1, п. 27-29), выполнить задания самостоятельной работы.

Цель урока: Изучить теорему Эйлера, выражающую топологические свойства многогранников.

Теоретический минимум и задачи

Многогранниками обычно называются тела, поверхности которых состоят из конечного числа многоугольников, называемых гранями многогранника. Стороны и вершины этих многоугольников называются соответственно ребрами и вершинами многогранника.

Многогранник называется выпуклым, если он является выпуклой фигурой, т. е. вместе с любыми двумя своими точками содержит и соединяющий их отрезок.

На рисунке 1 приведены примеры выпуклых и невыпуклых многогранников.

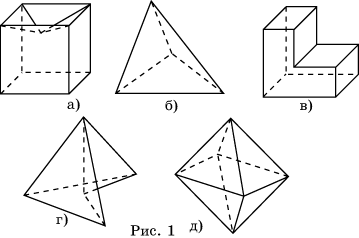
Рассмотрим некоторые свойства выпуклых многогранников.

Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.

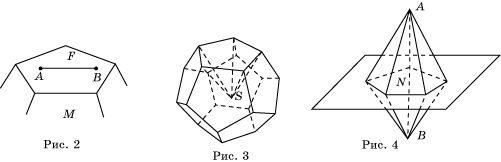
Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника (рис. 3).

Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани (рис. 4).

Для выпуклых многогранников имеет место свойство, связывающее число его вершин, ребер и граней, доказанное в 1752 году Леонардом Эйлером, и получившее название теоремы Эйлера.

Прежде чем его сформулировать рассмотрим известные нам многогранники и заполним следующую таблицу, в которой В - число вершин, Р - ребер и Г - граней данного многогранника:

Название многогранника	В	Р	Г
Треугольная пирамида	4	6	4
Четырехугольная пирамида	5	8	5
Треугольная призма	6	9	5
Четырехугольная призма	8	12	6
n-угольная пирамида	n+1	2n	n+1
n-угольная призма	2n	3n	n+2
n-угольная усеченная пирамида	2n	3n	n+2

Из этой таблицы непосредственно видно, что для всех выбранных многогранников имеет место равенство В - Р + Г = 2. Оказывается, что это равенство справедливо не только для этих многогранников, но и для произвольного выпуклого многогранника.

12 3 Следующая ⇒