Контакты

Случайная статья

Тригонометрическая форма записи комплексного числа. Модуль и аргумент

⇐ ПредыдущаяСтр 2 из 2

Тригонометрическая форма записи комплексного числа. Модуль и аргумент

Определение 2. Модуль комплексного числа 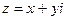обозначается 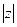и определяется по формуле .

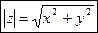Модуль числа z равен длине вектора : .

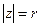Пример 4. Найти модули комплексных чисел 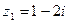и .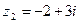

Решение. , .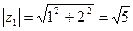

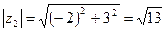Определение 2. Аргументом комплексного числа 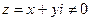называется угол между положительным направлением действительной оси и радиус-вектором с началом в точке O(0; 0) и концом в точке A(x; y). Угол считается положительным, если отсчёт ведётся против часовой стрелки, и отрицательным, если отсчёт производится по часовой стрелке.

Обозначение: , .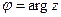

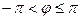Заданием модуля и аргумента комплексное число определяется полностью.

Справедливы формулы: 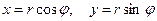. (1)

Отсюда комплексное число 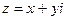может быть представлено в форме:

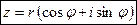. (2)

Формула (2) называется тригонометрической формой записи комплексного числа .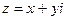

Пример 5. Дан модуль комплексного числа r = 2 и его аргумент 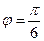. Найдите действительную и мнимую части комплексного числа.

Решение. По формулам (1) 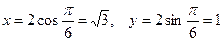, тогда .

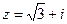Пример 6. Дано комплексное число 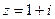. Найдите его модуль и аргумент.

Решение. x=1, y=1, 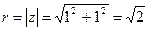. По формулам (1) получаем: .

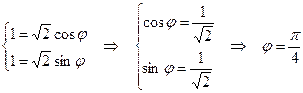Задачи.

1. Решите уравнения:

1)

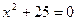
2)

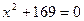
3)

4)

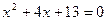
5)

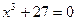
6)

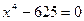
7)

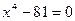
8)

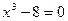
2. Выполните действия:

1)

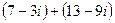
2)

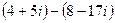
3)

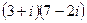
4)

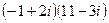
5)

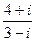
6)

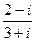
7)

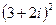
8)

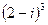
3. Следующие комплексные числа изобразите векторами, определите их модули и аргументы и запишите в тригонометрической форме:

1) z = 3

2) z = -5

3) z = 4i

4)

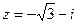
5) z = 1 + i

6)

⇐ Предыдущая 12

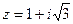
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.