Комплексные числа и операции над ними

Для решения алгебраических уравнений множества действительных чисел R недостаточно (например, уравнения и не имеют действительных корней). Для преодоления указанного затруднения вводят множество комплексных чисел C ( ). Решение уравнения обозначается через i и называется мнимой единицей, таким образом , . Уравнение имеет два комплексных корня .

Пример 1. 1) Решите уравнение .

Решение. Находим дискриминант и корни уравнения , .

2) Решите уравнение .

Решение. Находим дискриминант и корни уравнения , .

3) Решите уравнение .

Решение. ,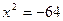

4) Решите уравнение .

Решение. 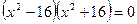, или . Тогда , .

Определение 1. Комплексным числом называется выражени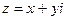е , где , , i – символ мнимой единицы. Число x называется действительной частью, а число y - мнимой частью комплексного числа 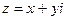. Два комплексных числа и , отличающиеся только знаком мнимой части, называются сопряжёнными.

Для комплексных чисел вводятся понятия равенства и операции сложения, вычитания, умножения и деления:

1) два комплексных числа и равны тогда и только тогда, когда , ;

2) комплексное число равно нулю тогда и только тогда, когда x=0, y=0;

3) суммой (разностью) чисел и называется число (в случае разности );

4) произведением чисел и называется число ;

5) деление комплексных чисел определяется как действие, обратное умножению: если , где , , то x и y должны быть такими, чтобы выполнялось равенство .

Пример 2. Даны комплексные числа , . Найдите их сумму и разность.

Решение. , .

Пример 3. Даны комплексные числа , . Найдите их произведение и частное.

Решение.

Геометрическое изображение комплексных чисел

Всякое комплексное число можно изобразить на плоскости XOY в виде точки A(x; y), и обратно, всякую точку A(x; y) плоскости XOY можно рассматривать как геометрический образ комплексного числа . При этом ось OY называют мнимой осью, а ось OX – действительной осью. Удобно считать геометрическим изображением комплексного числа вектор .

12 Следующая ⇒