
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение квадратных неравенств. Повторение.
АЛГЕБРА
Решение квадратных неравенств. Повторение.
Параграф 40.
Пусть у нас есть неравенство ах2+bx+c> 0 и пусть а> 0
1)Разберём сначала случай, когда существуют x1< x2 - корни уравнения ax2+bx+c=0

 Тогда ax2+bx+c=a(x-x1)(x-x2) и неравенство сводится к неравенству a(x-x1)(x-x2)> 0, а оно в свою очередь к системам неравенств (напоминаю, что a> 0)
Тогда ax2+bx+c=a(x-x1)(x-x2) и неравенство сводится к неравенству a(x-x1)(x-x2)> 0, а оно в свою очередь к системам неравенств (напоминаю, что a> 0)
x-x1> 0 x-x1< 0
x-x2> 0 или x-x2< 0 тогда, если х1< x2, то решением неравенства будет множество 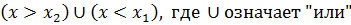
2) Очевидно, что неравенство ax2+bx+c< 0 при a> 0 и x1< x2 имеет решением множество x1< x< x2
3) Если неравенство нестрогое, то знаки “> ” и “< ” в решении надо заменить на знаки “ 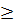 ” и “
” и “ 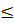 ”.
”.
4) Если a< 0, то умножая неравенство на (-1), получим неравенство вида (1) или (2).
5) Если корней уравнения ax2+bx+c=0 не существует, то либо ax2+bx+c> 0 при любых х, либо ax2+bx+c< 0 при любых х. При а> 0 и при отсутствии корней ax2+bx+c всегда положителен, а при a< 0 – всегда отрицателен.
6) Если корень уравнения ax2+bx+c=0 единственный и равен х1, то ax2+bx+c=a(x-x1)2 и при а> 0 ax2+bx+c всегда положителен кроме х=х1, а при а< 0 ax2+bx+c всегда отрицателен кроме х=х1.
Разберём несколько примеров
1) 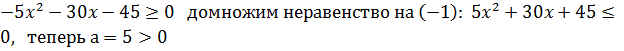
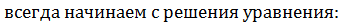
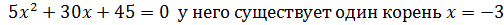
Следовательно неравенство 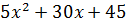 =5(х+3)2
=5(х+3)2 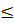 0 имеет одно решение х=-3
0 имеет одно решение х=-3
2) 3x2+x+10> 0
Уравнение 3x2+x+10 решений не имеет, так как дискриминант D=1-4 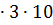 =-119< 0; 3> 0 => 3x2+x+10> 0 при любых х.
=-119< 0; 3> 0 => 3x2+x+10> 0 при любых х.
3) 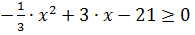
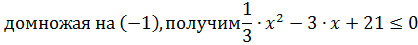
Дискриминант D=32- 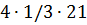 =-19< 0 => ( так как 1/3> 0) =>
=-19< 0 => ( так как 1/3> 0) => 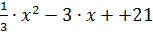 > 0 => решений нет.
> 0 => решений нет.
4) 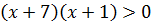
Квадратный трёхчлен уже разложен на множители, корни х1=-7< x2=-1 => решение неравенства: x< -7 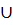 x> -1 (можно так: х< -7 или x> -1).
x> -1 (можно так: х< -7 или x> -1).
5) –x2+3x+4> 0
Сначала домножаем на (-1): x2-3x-4< 0, затем решаем уравнение x2-3x-4=0 => x1=-1< x2=4 => решение неравенства: -1< x< 4.
6) 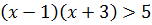
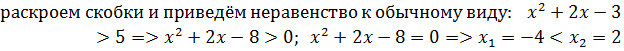
следовательно, решение неравенства: x< -4 или x> 2.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|