Хелпикс

Главная

Контакты

Случайная статья



2. Актуализация знаний по теме

Стр 1 из 2Следующая ⇒


 

Дата: 18. 03

Тема: Анализ контрольной работы

Цель урока: Обобщение и систематизация знаний по теме.

Задачи:

Образовательные:

- учащиеся должны знать и уметь применять свойства числовых неравенств;

- применять свойства при доказательстве неравенств;

- уметь видеть «свойства»;

Развивающие:

- способствовать развитию мыслительных процессов;

- способствовать развитию абстрактного мышления;

- развивать познавательные способности.

- развивать навыки самостоятельной работы;

- развивать интерес к предмету.

Воспитательные:

- воспитывать сознательное отношение к учению;

- воспитывать познавательную активность учащихся;

- воспитывать чувство личной ответственности в коллективной работе;

- воспитывать творческую, всесторонне-развитую личность.

Ход урока

1. Организационный момент.

2. Актуализация знаний по теме

1. Сложите почленно неравенства:

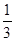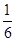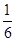а) 0< 5 и ־ 1 < 7; б) -2. 5 > 1. 5 и 2. 5 > 0. 3; в) - <   и -  < 0;

- 1 < 12                             0 > 1, 8                      -  <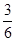

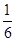
2. Перемножьте почленно неравенства:

а) 25> 10 и 2> 1; б) 101 < 103 и 10< 20;   в) 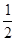 >  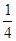 и  >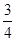

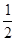
        50> 10                 1010< 2060                      >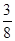  

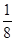
3. Зная, что 5 < х < 6 и -3 < у < -1, оцените:

а) х + у;        б) х - у;            в) ху;                       г) ;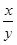

2< х + у < 5 8 < х – у < 7   -15 < ху < - 6    - 5/3 < 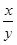 < - 6

4. Докажите неравенство:

а) а(а + 12) + 6 > 12а;                           б) (в - 4)(в + 4) + 18 > 0;

а2 + 12а + 6 – 12а > 0                            в2 – 16 + 18 > 0   

а2 + 6 > 0 верно при любом а              в2 + 2 > 0 верно при любом в

Задача 1. Оцените периметр и площадь прямоугольника со сторонами х(см) и у(см), если известно, что 4, 7 < х < 4, 8 и 5, 4 < у < 5, 5

    Р = 2 ∙ (х + у)                                   S = х ∙ у

   4, 7 < х < 4, 8                                     4, 7 < х < 4, 8 

   5, 4 < у < 5, 5                                     5, 4 < у < 5, 5

                 10, 1 < х + у < 10, 3                            25, 38< х ∙ у < 26, 4

          20, 2 < 2 ∙ (х + у) < 20, 6                     25, 38 < S < 26, 4

               20, 2 < Р < 20, 6 

Задача 2.     К каждому из чисел 6, 5, 4, 3 прибавили одно и тоже число в. Сравните произведение крайних членов получившейся последовательности с произведением средних членов.

   Решение:

Получим числа 6 + в; 5 + в; 4 + в; 3 + в;

Сравним произведения: (6 + в) ∙ (3 + в) и (5 + в)∙ (4 + в)

Рассмотрим разность: (6 + в) ∙ (3 + в) − (5 + в) ∙ (4 + в) =

                                         = 18 + 6в + 3в + в2 − 20 – 4в – 5в – в2 = - 2 < 0

т. к как разность отрицательна, то первое выражение меньше второго.

                                                        Ответ: (6 + в) ∙ (3 + в) < (5 + в)∙ (4 + в)           

Задача 3. Даны четыре последовательных натуральных числа. Сравните сумму квадратов последних чисел с удвоенным произведением двух средних чисел.

    Решение:

Пусть даны натуральные числа х, х +1, х + 2, х + 3;

Сравним х2 + (х + 3)2 и 2 ∙ (х + 1)(х + 2)

Рассмотрим разность: х2 + (х + 3)2 − 2 ∙ (х + 1)(х + 2) =

                                          = х2 + х2 + 6х + 9 – 2х2 -4х – 2х – 4 = 5 > 0

т. к разность положительна, значит, х2 + (х + 3)2 > 2 ∙ (х + 1)(х + 2)

                                                   

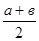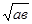
Задача 4. Докажите, что среднее арифметическое двух неотрицательных чисел меньше, чем их среднее геометрическое, т. е       ≥         (а ≥ 0 и в ≥ 0).

   Решение:

Равенство возможно лишь при а = в

 

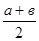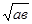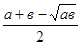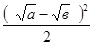
         −  =  = ≥ 0                  

      

верно при а ≥ 0 и в ≥ 0, т. к как числитель неотрицателен, а знаменатель 2 > 0 (положителен).  


12Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.