НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ. Аналогично,. Т.е. вычисляются несобственные интегралы также, как и обычные определенные, только со специальным оформлением: знак «- ∞» заменяем буквой а , знак «+∞» - буквой b. А перед знаком интеграла ставится знак

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Несобственным интегралом первого рода от функции 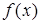в интервале [a, +∞ ) называется предел интеграла при :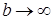

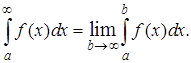
Если указанный предел существует и равен числу, то несобственный интеграл называется сходящимся, а если не существует или равен бесконечности, то расходящимся.

Если известна первообразная 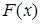для подынтегральной функции 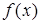, то легко установить, сходится несобственный интеграл или расходится. С помощью формулы Ньютона – Лейбница имеем

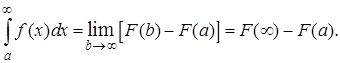
Аналогично,

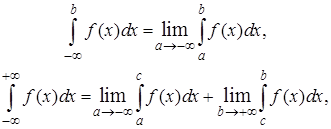
Т. е. вычисляются несобственные интегралы также, как и обычные определенные, только со специальным оформлением: знак «- ∞ » заменяем буквой а, знак «+∞ » - буквой b. А перед знаком интеграла ставится знак .

Пример 1. Вычислить несобственный интеграл (если он сходится).

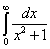
Решение. Подынтегральная функция непрерывна в каждой точке, поэтому определённый интеграл от неё на отрезке [0, b] существует при всяком b. Находим этот интеграл:

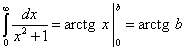По определению, данный несобственный интеграл сходится и его значение равно:

.

Пример 2. Вычислить несобственный интеграл (если он сходится).

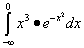
Решение. Находим предел данного интеграла:

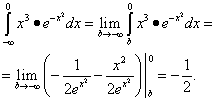
Вывод: данный несобственный интеграл сходится, а его значение равно -1/2.

Пример 3. Вычислить несобственный интеграл 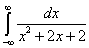с двумя бесконечными пределами (если он сходится).

Решение. На основании определения несобственного интеграла с двумя бесконечными пределами представляем данный интеграл как сумму двух несобственных интегралов:

.

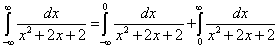Преобразуем подынтегральное выражение к форме 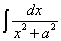, с помощью выделения полного квадрата:

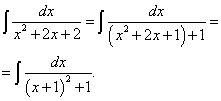
По формуле 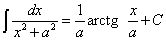находим:

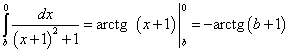
Предел этого интеграла существует:

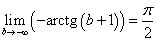
Второй интеграл, составляющий сумму, выражающую исходный интеграл:

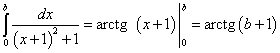
Предел этого интеграла также существует:

.

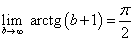Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

.

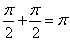Несобственным интеграломвторого рода от функции 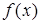, непрерывной при 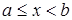и неограниченной при 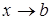, называется предел интеграла :

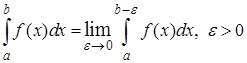Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то расходящимся.

Аналогично, если функция 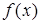претерпевает бесконечный разрыв только в левом конце x=a отрезка 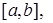то

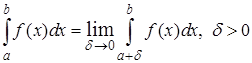Если функция 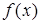претерпевает бесконечный разрыв в некоторой точке x=с, принадлежащей отрезку 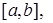то может быть определен несобственный интеграл

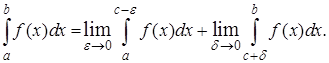
Пример 4. Вычислить несобственный интеграл 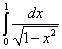(если он сходится).

Решение. Подынтегральная функция непрерывна в каждой точке полуотрезка [0, 1]. В точке x = 1 функция обращается в бесконечность. Если взять значение чуть меньше, чем b на некоторую малую величину 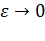, то на [0, b - 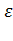] подынтегральная функция непрерывна и, следовательно, существует интеграл.

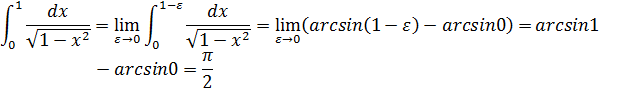
Следовательно, несобственный интеграл сходится и равен

Оценка несобственных интегралов.

12 Следующая ⇒