
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Три правила нахождения первообразных
Три правила нахождения первообразных
Правило №1: Если F есть первообразная для функции f, а G – первообразная для g, то F+G – есть первообразная для f+g.
(F(x) + G(x))’ = F’(x) + G’(x) = f + g
Правило №2: Если F – первообразная для f, а k – постоянная, то функция kF – первообразная для kf.
(kF)’ = kF’ = kf
Правило №3: Если F – первообразная для f, а k и b– постоянные ( 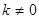 ), то функция
), то функция
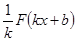 - первообразная для f(kx+b).
- первообразная для f(kx+b).
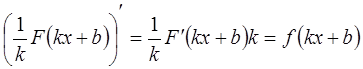
3. Вернемся к теореме 1 и выведем новое определение.
Определение 2: Выражение F(x) + C, где C - произвольная постоянная, называют неопределенным интегралом и обозначают символом
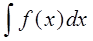
Из определения имеем:
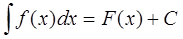 (1)
(1)
Неопределенный интеграл функцииf(x), таким образом, представляет собой множество всех первообразных функций дляf(x).
В равенстве (1) функциюf(x) называется подынтегральной функцией, а выражение f(x)dx– подынтегральным выражением, переменную x – переменной интегрирования, слагаемое C - постоянной интегрирования.
Интегрирование представляет собой операцию, обратную дифференцированию. Для того чтобы проверить, правильно ли выполнено интегрирование, достаточно продифференцировать результат и получить при этом подынтегральную функцию.
Свойства неопределенного интеграла.
Опираясь на определение первообразной, легко доказать следующие свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подынтегральной функции, то есть если 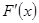 = f(x), то
= f(x), то
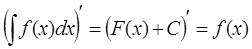
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
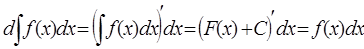
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
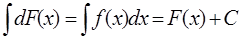
4. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов

5. Постоянный множитель можно выносить за знак интеграла, то есть если a=const, то
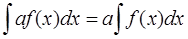
4. Таблица простейших интегралов
1. 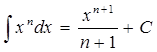 , (n
, (n  -1) 2.
-1) 2. 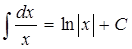
3. 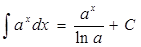 4.
4. 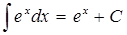
5. 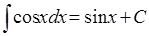 6.
6. 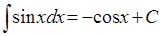
Интегралы, содержащиеся в этой таблице, принято называть табличными. Отметим частный случай формулы 1:
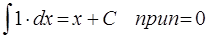
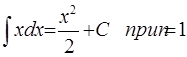
Приведем еще одну очевидную формулу:
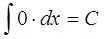 ,
,
т. е. первообразная от функции, тождественно равной нулю, есть постоянная.
Задание: Сопоставьте интеграл функции и его первообразную:
| Интеграл | Первообразная |
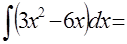
| 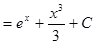
|

| 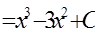
|

| 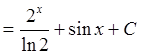
|

| 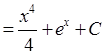
|

| 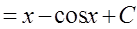
|
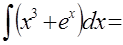
| 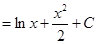
|
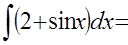
| 
|
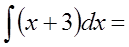
| 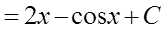
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|