Неопределенный интеграл, его свойства.

Символ 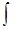введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S. Само слово «интеграл» придумано Бернулли в 1690 г. Оно происходит от латинского integro, которое переводится, как приводить в прежнее состояние, восстанавливать. Действительно, операция интегрирования обратная операции дифференцирования т. е. для того, чтобы проверить правильность нахождения интеграла необходимо продифференцировать ответ и получить подынтегральную функцию. Другими словами интегральное исчисление решает задачу: по заданной производной или дифференциалу неизвестной функции требуется определить эту функцию. Отсюда можно сделать вывод, который мы запишем в виде определения.

2. Определение 1: Функция F(x) называется первообразной для функции f(x) на отрезке [a; b], если во всех точках этого отрезка выполняется равенство 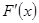= f(x) или dF(x)=f(x)dx

Так, функция F(x) = x^m является первообразной для f(x)=mx^m^-1, так как

(x^m)^’=mx^m^-1.

Точно также функция F(x) =ln x есть первообразная для f(х)= 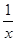, так как

(ln x)’= .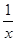

Признак постоянства функции:

Если F’(x)=0 на некотором промежутке I, то функция F – постоянна на этом промежутке, т. е. F(x)=C.

Все первообразные функции f можно записать в одну формулу, которую называют общим видом первообразных для функции f. Запишем это в виде теоремы.

Теорема: Любая первообразная для функции f на промежутке I может быть записана в виде F(x)+C, где F(x) – одна из первообразных для функции f(x) на промежутке I, C – произвольная постоянная.

Этому свойству можно придать геометрический смысл: графики любых двух первообразных для функции f получаются друг из друга параллельным переносом вдоль оси Oy.

12 Следующая ⇒