
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Локальная Ц.П.Т.. Ц.П.Т. Линдберга. Ц.П.Т. Ляпунова. Ц.П.Т. для мартингалов
Локальная Ц. П. Т.
В предположениях классической формулировки, допустим в дополнение, что распределение случайных величин {Xi}, i=1, n абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение также абсолютно непрерывно, и более того
 при n→ ∞,
при n→ ∞,
где  - плотность случайной величины
- плотность случайной величины 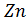 , а в правой части стоит плотность стандартного нормального распределения.
, а в правой части стоит плотность стандартного нормального распределения.
Результат классической центральной предельной теоремы справедлив для ситуаций гораздо более общих, чем полная независимость и одинаковая распределённость.
Ц. П. Т. Линдберга
Пусть независимые случайные величины Х1, Х2, …, Хn, … определены на одном и том же вероятностном пространстве и имеют конечные математические ожидания и дисперсии: E[Xi]=μ i, D[Xi]= 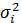 . Как и прежде построим частичные суммы Sn =
. Как и прежде построим частичные суммы Sn = 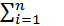 . Тогда в частности,
. Тогда в частности,
E[Sn] = mn = 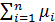 , D[Sn]=
, D[Sn]=  =
= 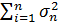
Наконец, пусть выполняется условие Линдеберга:
∀ ε > 0, 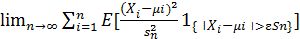
Тогда
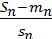 → N(0, 1) по распределению при n→ ∞.
→ N(0, 1) по распределению при n→ ∞.
Ц. П. Т. Ляпунова
Пусть выполнены базовые предположения Ц. П. Т. Линдеберга. Пусть случайные величины {Xi} имеют конечный третий момент. Тогда определена последовательность

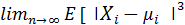 ]
]
Если предел 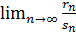 = 0 (условие Ляпунова) , то
= 0 (условие Ляпунова) , то
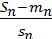 → N(0, 1) по распределению при n→ ∞.
→ N(0, 1) по распределению при n→ ∞.
Ц. П. Т. для мартингалов
Пусть процесс 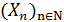 является мартингалом. Введём случайные процессы
является мартингалом. Введём случайные процессы 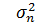 и
и 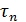 следующим образом:
следующим образом:
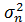 =E[
=E[ 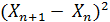 ∣ X1, …, Xn ] и
∣ X1, …, Xn ] и 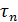 =min{ ∣
=min{ ∣  }.
}.
Тогда
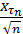 → N(0, 1) по распределению при n→ ∞.
→ N(0, 1) по распределению при n→ ∞.
Докажем центральную предельную теорему для случая одинаково распределенных случайных величин (в форме Ляпунова).
Теорема. Если Х1, Х2, …, Хn – независимые случайные величины, имеющие одно и то же распределение с математическим ожиданием m и дисперсией σ 2, то при увеличении n закон распределения суммы 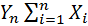 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
Доказательство. Докажем теорему для случая непрерывных случайных величин, применив аппарат характеристических функций. Согласно одному из свойств, характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых. Случайные величины имеют одну и ту же плотность распределения f(x), а значит, и одну и ту же характеристическую функцию υ х (t). Не нарушая общности, можно перенести начало отсчета всех случайных величин Х1, Х2, …, Хn в их общее математическое ожидание m, что равнозначно их центрированию и, значит, тому, что математическое ожидание каждой из них будет равно нулю.
Для доказательства теоремы найдем характеристическую функцию гауссовой случайной величины с нулевым математическим ожиданием и единичной дисперсией, плотность распределения которой
f(x)= 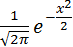
Характеристическая функция такой случайной величины
υ х(t)= 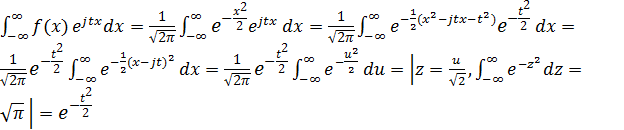 .
.
Получили, что характеристическая функция нормальной случайной величины X с mX = 0 и DX = σ 2X = 1 имеет вид
υ х(t)  . (1)
. (1)
По определению характеристическая функция случайной величины X
υ х(t)  (2)
(2)
Характеристическая функция случайной величины 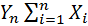 равна произведению n характеристических функций слагаемых, т. е.
равна произведению n характеристических функций слагаемых, т. е.

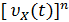 (3)
(3)
Разложим 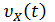 в окрестности точки t=0 в ряд Макларена, ограничившись тремя членами
в окрестности точки t=0 в ряд Макларена, ограничившись тремя членами
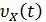 ≈
≈ 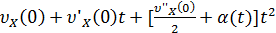 (4)
(4)
где 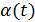 → 0 при t→ 0.
→ 0 при t→ 0.
Вычислим 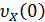 ,
,  ,
, 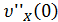 .
.
Так, 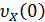 =
= 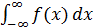 = 1 по свойству нормировки функции f (x).
= 1 по свойству нормировки функции f (x).
Продифференцируем выражение (2) по t
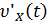 =
= 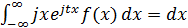
и получаем при t = 0
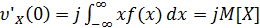 ,
,
а так как все Х1, Х2, …, Хn имеют одну и ту же плотность распределения f(x) и нулевое математическое ожидание, то 
Продифференцируем теперь (4): 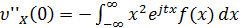 и соответственно при t = 0 получим
и соответственно при t = 0 получим
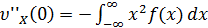 =
= 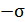 2
2
После подстановки в (3) имеем, что
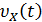 = 1-[
= 1-[  ]t2 (5)
]t2 (5)
Для случайной величины Yn докажем, что при увеличении n ее закон распределения приближается к нормальному закону распределения. Для этого перейдем к нормированной случайной величине Zn= 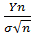 , которая линейно связана с Yn и удобна тем, что ее дисперсия равна единице для любого n. Если докажем, что случайная величина Zn имеет нормальное распределение, то это будет означать, что и величина Yn тоже распределена нормально.
, которая линейно связана с Yn и удобна тем, что ее дисперсия равна единице для любого n. Если докажем, что случайная величина Zn имеет нормальное распределение, то это будет означать, что и величина Yn тоже распределена нормально.
Докажем, что характеристическая функция 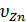 , однозначно определяющая плотность распределения случайной величины Zn, приближается к характеристической функции нормального закона с теми же, что и у Zn, параметрами:
, однозначно определяющая плотность распределения случайной величины Zn, приближается к характеристической функции нормального закона с теми же, что и у Zn, параметрами: 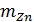 = 0;
= 0; 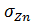 = 1.
= 1.
Найдем характеристическую функцию случайной величины Zn, используя свойства характеристических функций и выражения (1) и (4):
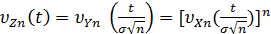 =
= 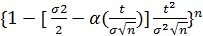
Прологарифмируем это выражение и получим ln 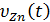 = n ln
= n ln 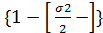
Пусть χ = 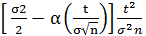 , и тогда ln
, и тогда ln 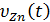 = n ln (1
= n ln (1 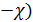
Если неограниченно увеличивать n, то величина 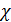 будет стремиться к
будет стремиться к
нулю. Поэтому разложим ln (1 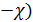 в ряд по степеням
в ряд по степеням 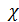 , ограничившись
, ограничившись
первым членом разложения, т. е. ln (1 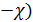 ≈
≈ 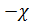 . Таким образом, получаем
. Таким образом, получаем 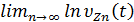 =
= 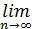 n
n 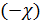 =
=  +
+  ] =
] = 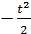 +
+  ≈
≈ 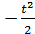
так как функция 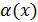 → 0, когда аргумент x=
→ 0, когда аргумент x= 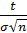 при n→ ∞.
при n→ ∞.
Получили, что 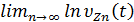 =
= 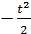 , следовательно,
, следовательно,
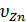 =
= 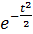
но это и есть характеристическая функция нормально распределенной случайной величины с нулевым математическим ожиданием и единичной дисперсией (см. выражение (1)). Следовательно, и линейно связанная со
случайной величиной Zn случайная величина Yn имеет нормальное раcпределение.
Примеры.
В книге Е. С. Вентцель «Теория вероятностей» (Москва: Наука, 1969) приведены две задачи на применение центральной предельной теоремы о том, что сумма случайных величин при определенных условиях может быть приближена нормальным законом.
Пример 1. По полосе укреплений противника сбрасывается 100 серий бомб. При сбрасывании одной такой серии математическое ожидание числа попаданий равно 2, а среднее квадратическое отклонение числа попаданий равно 1, 5. Найти приближенно вероятность того, что при сбрасывании 100 серий в полосу попадает от 180 до 220 бомб.
Решение. Представим общее число попаданий как сумму чисел попаданий бомб в отдельных сериях:
X = X1+ X2+ … + X100 = 
где  – число попаданий i-той серии.
– число попаданий i-той серии.
Условия центральной предельной теоремы соблюдены, так как величины X1, X2, …, X100 распределены одинаково. Будем считать число n = 100 достаточным для того, чтобы можно было применить предельную теорему (на практике она обычно применима и при гораздо меньших n). Имеем:
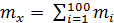 = 200,
= 200, 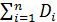 =
= 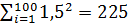
Применяя формулу, получим:
P(180 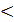 X
X 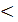 220) = Ф*(
220) = Ф*( 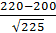 )
)  Ф*(
Ф*( 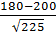 ) ≈ 0, 82
) ≈ 0, 82
т. е. с вероятностью 0, 82 можно утверждать, что общее число попаданий в полосу не выйдет за пределы 180/ 220.
Пример 2. Происходит групповой воздушный бой, в котором участвуют 50 бомбардировщиков и 100 истребителей. Каждый бомбардировщик атакуется двумя истребителями; таким образом, воздушный бой распадается на 50 элементарных воздушных боев, в каждом из которых участвует один бомбардировщик и два истребителя. В каждом элементарном бою вероятность сбития бомбардировщика равна 0, 4; вероятность того, что в элементарном бою будут сбиты оба истребителя, равна 0, 2; вероятность того, что будет сбит ровно один истребитель, равна 0, 5. Требуется: 1) найти вероятность того, что в воздушном бою будет сбито не менее 35% бомбардировщиков; 2) оценить границы, в которых с вероятностью 0, 9 будет заключено число сбитых истребителей.
Решение. 1) Обозначим Х- число сбитых бомбардировщиков;
X = 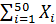 ,
,
где 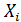 – число бомбардировщиков, сбитых в i-том элементарном бою.
– число бомбардировщиков, сбитых в i-том элементарном бою.
Ряд распределения величины имеет вид:
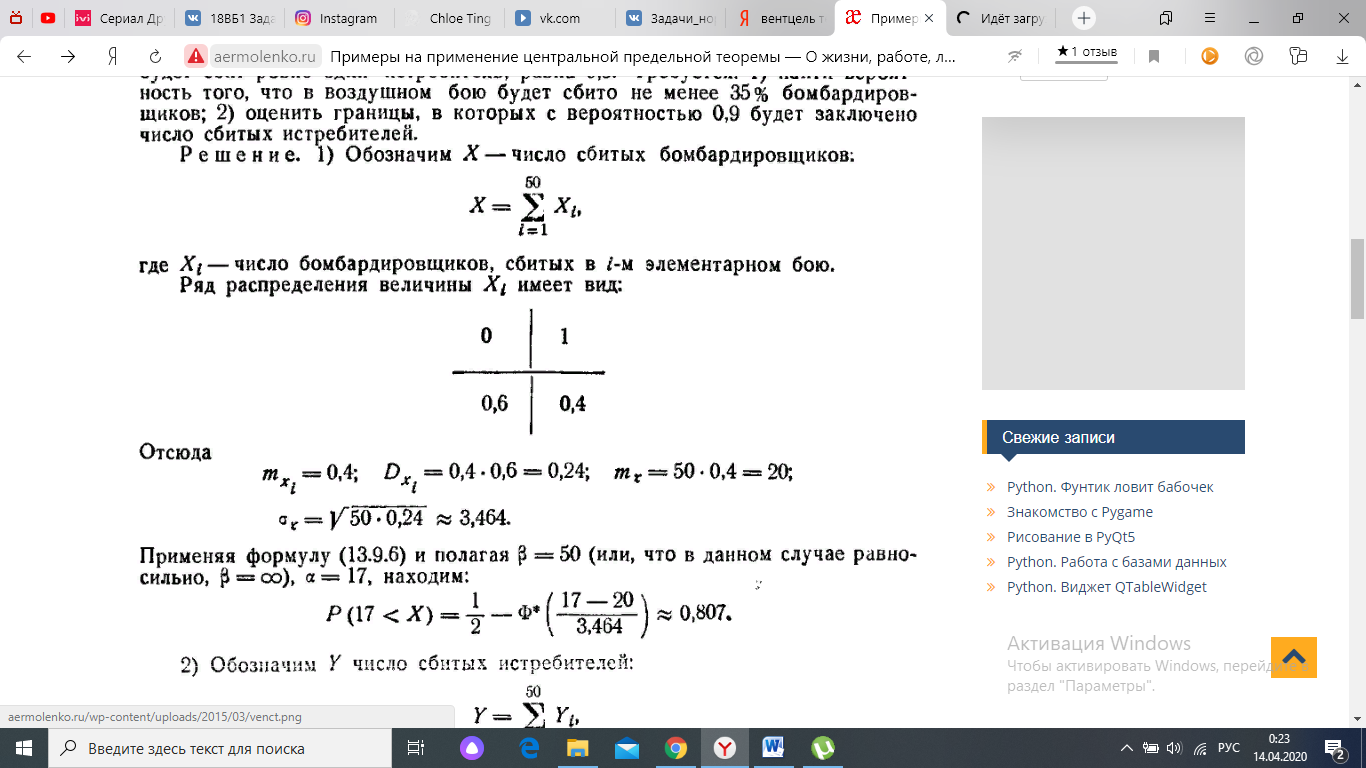
Отсюда
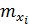 = 0, 4;
= 0, 4;  = 0, 4 * 0, 6 = 0, 24;
= 0, 4 * 0, 6 = 0, 24; 
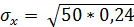 ≈ 3, 464.
≈ 3, 464.
Применяя формулу и полагая β = 50 (или, что в данном случае равносильно, β = ∞ ), α = 17, находим
P(17 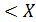 ) =
) =  – Ф*(
– Ф*( 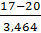 ) ≈ 0, 807
) ≈ 0, 807
2) Обозначим Y - число сбитых истребителей:
Y = 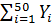 ,
,
где 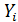 – число истребителей, сбитых в i-том элементарном бою.
– число истребителей, сбитых в i-том элементарном бою.
Ряд распределения величины имеет вид:
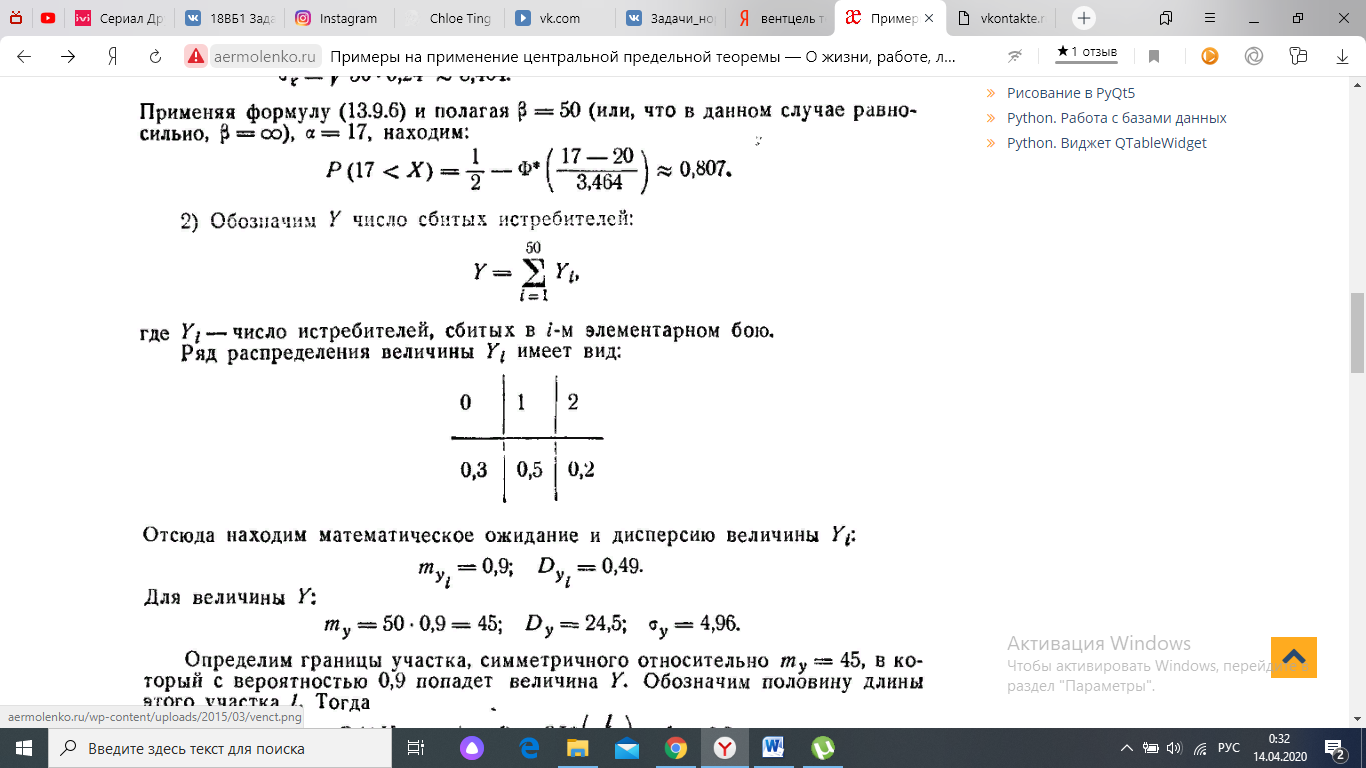
Отсюда находим математическое ожидание и дисперсию величины 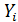
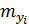 = 0, 9;
= 0, 9; 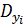 = 0, 49;
= 0, 49; 
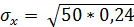 ≈ 3, 464.
≈ 3, 464.
Для величины Y:


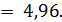
Определим границы участка, симметричного относительно 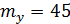 , в который с вероятностью 0, 9 попадет величина Y. Обозначим половину длины этого участка l. Тогда
, в который с вероятностью 0, 9 попадет величина Y. Обозначим половину длины этого участка l. Тогда
P( 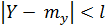 ) = 2Ф*(
) = 2Ф*( 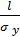 ) – 1 = 0, 9
) – 1 = 0, 9
Ф*( 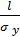 ) = 0, 95
) = 0, 95
По таблицам функции Ф*( 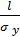 ) находим то значение аргумента, для которого Ф*(х) = 0, 95; это значение приближенно равно
) находим то значение аргумента, для которого Ф*(х) = 0, 95; это значение приближенно равно
х = 1, 645,
т. е.
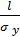 = 1, 645,
= 1, 645,
откуда
l = 8, 14 ≈ 8.
Следовательно, с вероятностью около 0, 9 можно утверждать, что число сбитых истребителей будет заключено в пределах 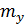 ± l, т. е. в пределах от 37 до 53.
± l, т. е. в пределах от 37 до 53.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|