кафедра «Высшая и прикладная математика»

Стр 1 из 2Следующая ⇒

Министерство образования и науки Российской Федерации

ФГБОУ ВО «Пензенский государственный университет»

кафедра «Высшая и прикладная математика»

Доклад

по дисциплине «Теория вероятностей, математическая статистика и теория

случайных процессов»

«Центральная предельная теорема»

Выполнил: ст. гр. 18ВБ1

Тархова Д. А.

Проверил: доцент каф. ВиПМ, к. ф. -м. н.

Бойкова А. И.

Пенза, 2020

Центральные предельные теоремы (Ц. П. Т. ) — класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения.

Нормальное распределение — наиболее распространенное в природе распределение непрерывных величин.

Классическая формулировка Ц. П. Т.

Пусть Х₁, Х₂, …, Х_n, … бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ ² соответственно. Пусть S_n = 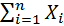. Тогда

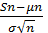→ N(0, 1) по распределению при n→ ∞ .

Обозначив символом X̅ выборочное среднее первых n величин, то есть X̅ = 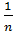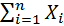, мы можем переписать результат центральной предельной теоремы в следующем виде:

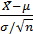по распределению при n→ ∞.

12 Следующая ⇒