Хелпикс

Главная

Контакты

Случайная статья



1. Решаем задачу при коэффициенте сопротивления h = 2

Стр 1 из 2Следующая ⇒


 

Министерство высшего образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Нижегородский государственный архитектурно-строительный университет»

 

 

 

 

Инженерно-строительные факультет

 Кафедра математики

 

 

 

РГР 1

 

 

 

 

 

 

Выполнил:

Студент 1 курса, гр. М. С – 9/06                                                                       Морозов Д. Е.

 

Проверил:                                                                                                           Коган М. М.

 

 

 

 

 

Нижний Новгород

2020

Решение.

Зададимся математической моделью движения лодки, при которой лодка движется с постоянной скоростью v, силы сопротивления движения компенсируется силой движущей силы. Момент сил (относительно центра масс лодки) возникает в случае, когда набегающий на лодку поток отклоняется от продольной оси лодки. Угол отклонения обозначим φ, соответственно скорость вращения судна будет равна первой производной от этого угла 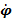. При вращении в лодке возникает момент равный - 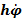. Тогда изменение угла поворота лодки, без учета воздействия руля, будет описываться уравнением:

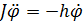,                                              (1)

J – момент инерции лодки.

При добавлении в модель лодки руля угол отклонения которого примем за 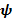, тогда уравнение (1) примет вид:

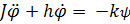.                                     (2)

Из этой формулы мы выразим угол поворота руля 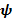, и в полученном выражении заменим коэффициенты пр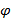и  и 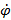 на a и b соответственно. Получим:

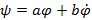.                                                         (3)

Следующим шагом подставляем выраженный угол поворота руля в уравнение (2) и находим что:

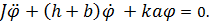                                       (4)

Состояние равновесия линейного осциллятора, описанного этим дифференциальным уравнением, будет устойчивым, тогда, когда все коэффициенты его характеристического уравнения

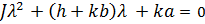                                                    (5)

положительные, т. е. при выполнении условий 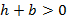, , 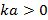соответственно:

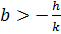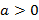,                                                              (6)

Вводим исходные данные для произведения расчетов:

· k=1;

· J = 1

· h = 2 (вариант 1)

· h = -3 (вариант 2)

1. Решаем задачу при коэффициенте сопротивления h = 2

Запишем уравнение движения лодки с рулем:

,

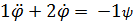Сравниваем это выражение с уравнением осциллятора с устойчивым положением равновесия:

,

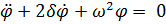и находим что для приведения уравнения движения к состоянию устойчивого равновесия нужно что бы

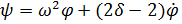
Из известного нам выражения (3) на ходим коэффициенты a и b:

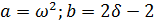
Из условия (6) получаем:

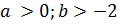
Область устойчивости:

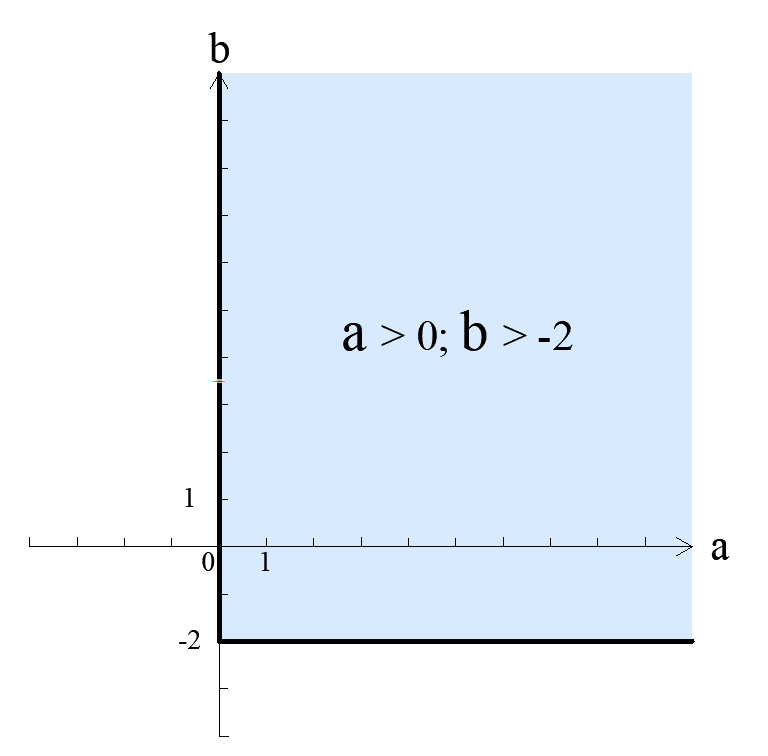
Из полученной области значений коэффициентов возьмем b = -1, a = 2 и подставим их в уравнение:

,

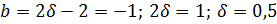
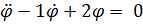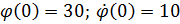
Найдем его решения:

· Записываем характеристическое уравнение:

,

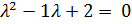· Находим его корни:

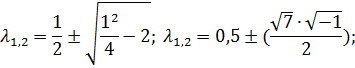
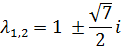
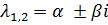
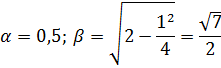
· Находим общее решение дифференциального уравнения:

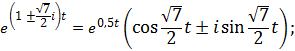
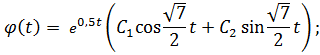
· Находим частное решение дифференциального уравнения:

При 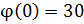 получим ;

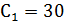Затем найдем первую производную и подставим начальные условия для нее

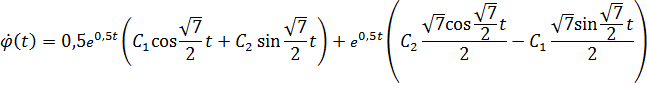
При 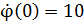 получим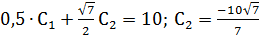

Тогда частное решение дифференциального уравнения примет вид:


12Следующая ⇒
  

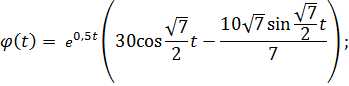
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.