I. Организационный момент. II. Устная работа. III. Работа по теме урока

Алгебра 7 класс

Тема: Линейное уравнение с двумя переменными.

График линейного уравнения с двумя переменными.

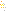Цели урока:

Образовательная: знать какое уравнение называется линейным уравнением с двумя переменными, что является решением такого уравнения, какие уравнения с двумя переменными называются равносильными, свойства уравнений, что называется графиком линейного уравнения. Уметь выражать одну переменную через другую, определять является ли пара чисел решением уравнения, строить график линейного уравнения с двумя переменными.

Оборудование:

Компьютер

Учебник

Ход урока

I. Организационный момент

II. Устная работа

Ответить на вопросы:

- Что такое уравнение?

- Что значить решить уравнение?

- Что такое корень уравнения?

- Приведите пример уравнения

- Решите уравнения:

5х=10; 1, 5х-3=0; 64+4х=40; 3х+2у=12

III. Работа по теме урока

Тема сегодняшнего урока: «Линейное уравнение с двумя переменными и его график»

Вы узнаете

какое уравнение называется линейным уравнением с двумя переменными

что является решением такого уравнения

какие уравнения с двумя переменными называются равносильными

свойства уравнений

что называется графиком линейного уравнения

- Уравнение ax + b = 0, где a ≠ 0, называют линейным уравнением с одной переменной x (или линейным уравнением с одним неизвестным x). Решить его, т. е. выразить x через a и b, мы с вами умеем:

ax=-b

x=-b/a

Рассмотрим такую реальную ситуацию.

Из городов A и B, расстояние между которыми 500 км, навстречу друг другу вышли два поезда, каждый со своей постоянной скоростью. Известно, что первый поезд вышел на 2 ч раньше второго. Через 3 ч после выхода второго поезда они встретились. Чему равны скорости поездов?

Составим математическую модель задачи. Пусть x км/ч — скорость первого поезда, y км/ч — скорость второго поезда. Первый был в пути 5 ч и, значит, прошел путь 5x км. Второй поезд был в пути 3 ч, т. е. прошел путь Зy км. Их встреча произошла в пункте C. На рисунке представлена геометрическая модель ситуации

На алгебраическом языке ее можно описать так: 5x +3y=500

Или 5x +3y-500=0

Эту математическую модель называют линейным уравнением с двумя переменными x, y.

Вообще,

ax+by+c=0 где a, b, c — числа, причем a ≠ 0, b ≠ 0, — линейное уравнение с двумя переменными x и y (или с двумя неизвестными x и y). Решением уравнения ax +by + c = 0 называют всякую пару чисел (x; y), которая удовлетворяет этому уравнению, т. е. обращает равенство с переменными ax + by + c = 0 в верное числовое равенство.

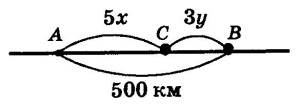
Пример 1. Изобразить решения линейного уравнения с двумя переменными x+ y - 3 = 0 точками в координатной плоскости xOy.

Решение. Подберем несколько решений заданного уравнения, т. е. несколько пар чисел, которые удовлетворяют уравнению: (3; 0), (2; 1), (1; 2), (0; 3), (-2; 5).

Построим в координатной плоскости xOy точки A (3; 0), B (2; 1), C (1; 2), D (0; 3), E (-2; 5) (Обратите внимание: все эти пять точек лежат на одной прямой, проведем ее.

Говорят, что прямая является графиком уравнения x + y - 3 = 0. Говорят также, что прямая — геометрическая модель уравнения x + y - 3 = 0 (или x + y = 3).

Подведем итоги:

Реальная ситуация (словесная модель)	Алгебраическая модель	Геометрическая модель
Сумма двух чисел равна 3	x + y = 3 (линейное уравнение с двумя переменными)	прямая на рисунке (график линейного уравнения с двумя переменными)

Теорема 1. Графиком любого линейного уравнения ax + by + c = 0 является прямая.

12 Следующая ⇒