Линейные уравнения с двумя переменными

Линейные уравнения с двумя переменными

Определение: Линейные уравнения с двумя переменными – это уравнение вида ax+by+c=0, где x,y - переменные, a,b,c – некоторые числа.

Например: 5х + 2у = 10; -7х+у = 5; х – у =2

Определение: Решение уравнения с двумя переменными – это пара значений переменных, обращающая это уравнение в верное равенство.

2х – 3у = 10

Если х=4, у=1,5 , то 2 ∙ 4 – 3 ∙ 1,5 = 10

8 – 4,5 = 10

3,5 = 10 неверно,

т.е. пара чисел (4; 1,5) не является решением уравнения.

Определение: Равносильные уравнения – это уравнения, имеющие одни и те же решения или не имеющие их.

Свойства уравнений:

1.В уравнении можно перенести слагаемое из одной части уравнения в другую, изменив его знак.

2.Обе части уравнения можно множить или разделить на одно и то же отличное от нуля число.

Например:

Выразить одну переменную через другую:

1) 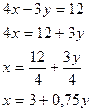2х +у = 5 2) 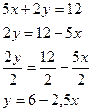3)

у = 5 -2х

График линейного уравнения с двумя переменными

Определение: График уравнения с двумя переменными – это множество всех точек координатной плоскости, координаты которых являются решениями этого уравнения.

1. Пример: 3х + 2у = 6, где а=3, b=2, c=6

План 1) Выразить переменную у

2у = 6-3х

у =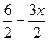

у = 3 – 1,5х

у = -1,5х +3 линейная функция вида y = kx + b,

где k = -1,5 ; b=3

2) Составить таблицу значений х и у

х
у

3) Построить график

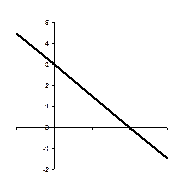
2. Частные случаи построения графика ax + by = c

a = 0, by = с у =	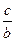b = 0, ax = с x =	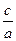a = 0, b = 0 0x+ 0y = с нет решения	a = 0, b = 0, с = 0 0x+ 0y = 0 множество решений
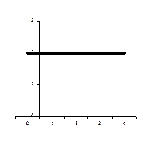
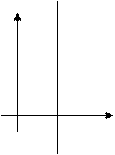у = 2	х = 2	Графика не существует	График – вся координатная плоскость

Решение систем уравнений с двумя переменными. Графический способ.

Определение: Система уравнений – это несколько уравнений, для которых находят общее решение.

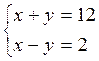
Определение: Решение системы уравнений с двумя переменными – это пара значений переменных, обращающая каждое уравнение в верное равенство.

Если х=7, у=5, то 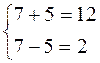, , 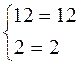верно,

т.е. (7; 5) – решение системы уравнений.

Определение: Решить систему – это значит найти все ее решения или доказать, что решений нет.

12 3 Следующая ⇒