- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Функции вычисления числовых характеристик матриц
Функции вычисления числовых характеристик матриц
last(v) – вычисление индекса последней компоненты вектора v;
length(v) – вычисление количества компонент вектора v;
rows(A) – вычисление числа строк в матрице А;
cols(A) – вычисление числа столбцов в матрице А;
max(A) – вычисление наибольшего элемента в матрице А;
min(A) – вычисление наименьшего элемента в матрице А;
sort(V) – сортировка элементов вектора V по возрастанию;
reverse (sort(v)) – сортировка элементов вектора V по убыванию;
csort (A,n) – сортировка элементов n – го столбца матрицы А по возрастанию (перестановкой строк);
rsort (A,n) – сортировка элементов n – ой строки матрица А по возрастанию (перестановкой столбцов);
mean(A) – среднее значение элементов матрицы А.
Рабочее задание
1. Запустить программу MathCad Prime .
2. Создать матрицы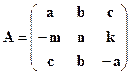 
, 
, 
, 
, 
, 
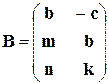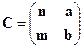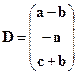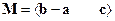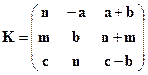из коэффициентов a, b, c, m, k, n в соответствии с вариантом задания.
3. Выполнить действия с матрицами в соответствии с вариантом задания (табл.). Разобраться с причинами невыполнения некоторых действий.
4. Отсортировать по возрастанию и убыванию вектор D.
5. Отсортировать по возрастанию вторую строку матрицы A.
6. Отсортировать по возрастанию первый столбец матрицы A.
7. Найти определители матриц А, C, K.
8. Найти обратные матрицы А, C, K.
9. Найти произведения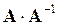 
, 
, 
.
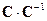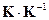10. Найти количества строк и столбцов для всех матриц.
11. Найти минимальные и максимальные элементы для всех матриц.
12. Найти средние значения элементов для всех матриц.
13. С помощью augment создать матрицу P из матриц A и B
14. С помощью submatrix выделить матрицу A из матрицы P.
15. С помощью staсk создать матрицуQ из матриц A иK.
16. С помощью submatrix выделить матрицу A из матрицы Q.
17. Транспонировать созданные матрицы P и Q.
18. С помощью функции diagсоздать диагональную матрицу из вектора D.
19. С помощью функции identityсоздать единичную матрицу 3-го порядка.
20. С помощью оператора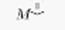 
и функции stack создать матрицу из первой строки матрицы А и третьей строки матрицы K.
21. С помощью оператора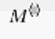 
и функции augment создать матрицу из второго столбца матрицы А и первого столбца матрицы K.
22. Умножить вектор Dна себя скалярно и векторно.
Таблица – Варианты заданий
| Номер варианта | Значение элементов матриц | Действия с матрицами |
| a=1; b=0.5; c=-1; m=2; k=-2.1; n=-0.8 | 1) A+A×K; 2) B×C; 3) M3; 4)A+m×K; 5)A×D; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M3; 4)D+m×K; 5)A×D+D×M; 6)K-2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A+B×M; 2) M×C; 3) B3; 4)C+m×K; 5)AB+D×K 6)D-3 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A-M; 2) B-a×C 3) M2-B; 4)D-×K; 5)A+7×D; 6)A-2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A2; 2) B×C+M; 3) n×M2; 4)D-K; 5)A×B-D×C; 6)D-2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A2+M; 2) B-M; 3) b×C-3; 4)D+3K; 5)A×K-D; 6)M-2 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|