Контакты

Случайная статья

Ответ: Корней нет. Ответ: решений нет. Ответ: - корни

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Ответ: Корней нет

3) 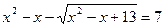добавим по 13 к обеим частям уравнения

ОДЗ: x²-x+13>0 для хÎ(-∞;∞), так как дискриминант соответствующего квадратного уравнения отрицательный, и следовательно график соответствующей квадратичной параболы не пересекает оси ОХ, и находится выше её, т.к. а>0

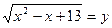- замена

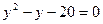
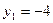- не является решением

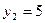
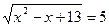
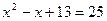
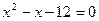
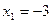
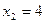
Проверка 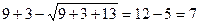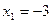- корень

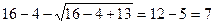
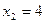- корень

Ответ: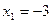

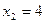
4)

ОДЗ:

х+6≥0 x ≥-6

х-7≥0 х ≥ 7 хÎ[7;∞)

(домножим обе части уравнения на )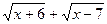

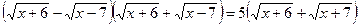
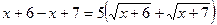
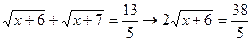
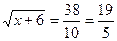
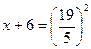
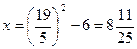=8,44- не удовлетворяет исходному уравнению в проверке.

Ответ: решений нет

5)

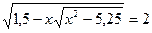
ОДЗ:

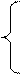х²-5,25≥0

……

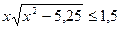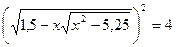
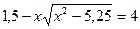
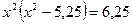
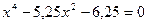замена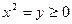

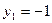- невозможно 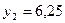, откуда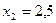

Проверка 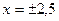в исходном выражении покажет, что 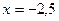- корень

Ответ: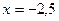

6)

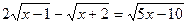
ОДЗ:

x-1≥0 x ≥1

х+2≥0 х ≥ -2 хÎ[1;∞)

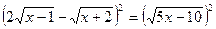
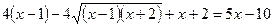
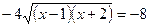
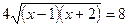
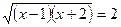
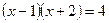
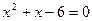
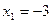
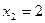
Проверка

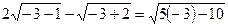- не имеет смысла 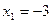- посторонний корень

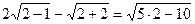- верно 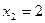- корень

Ответ: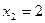

7)

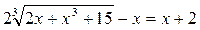
ОДЗ – поскольку в уравнении корень кубический, то подкоренное выражение может быть каким угодно, следовательно хÎ(-∞;∞)

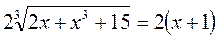- обе части уравнения сокращаем на 2 и возводим в куб

;

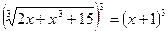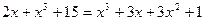
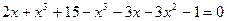
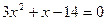
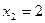
Проверку сделать самостоятельно!!! -…..

Ответ: - корни

8)

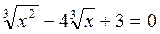
ОДЗ: хÎ(-∞;∞)

используем формулу: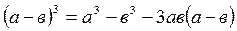

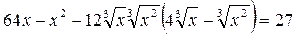
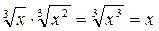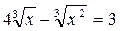Так как и имеем

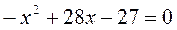
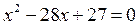
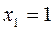
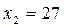- корни

Проверку сделать самостоятельно!!! -…..

Ответ:

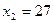
9) способ замены:

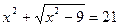
ОДЗ: х²-9≥0, (х-3)(х+3)≥0 далее методом интервалов, который применяется при сравнении с нулем частного или произведения алгебраических выражений:

находим значения, в которых получаются нулевые значения в скобках –

это х-3=0, х=3 или х+3=0, х= -3,

затем отмечаем на числовой прямой интервалы, в которых сохраняется знак, т.е.

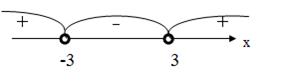
Следовательно хÎ(-∞;-3]È[3;∞)

отнимем 9 в обеих частях

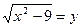, вводим замену , где у≥0

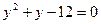
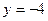
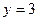
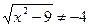- невозможно

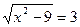
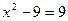
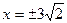
Ответ: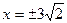

⇐ Предыдущая 123 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.