
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Ірраціональні рівняння, системи та засоби їх розв’язання
Тема: Ірраціональні рівняння, системи та засоби їх розв’язання
О: Уравнение, в котором неизвестное содержится под знаком радикала, называется иррациональным
Способы решения иррациональных уравнений:
А) возведение обеих частей уравнения в одну и ту же степень с обязательной проверкой из-за появления посторонних корней с исследованием ОДЗ – области допустимых значений для исключения посторонних корней
1) 
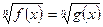
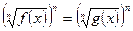
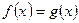
При п – четном 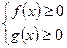
п – нечетном 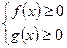 или
или 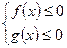
2) 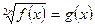
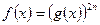 при
при 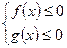
Б) введение новой переменной (способ замены)
В) метод равносильных преобразований
– умножение или деление на одно и то же число
- перенос членов уравнения из одной части уравнения в другую с изменением знака
- прибавление к обеим частям уравнения одного и того же числа
Иногда, не решая иррациональные уравнения, можно выяснить имеет оно корень или нет.
№ 72 Не решая, объяснить – почему в уравнении нет корней:
1) 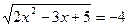 - арифметический квадратный корень неотрицательный
- арифметический квадратный корень неотрицательный
2) 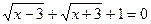
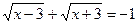 - в левой части – сумма арифметических квадратных корней, а в правой – отрицательное число – невозможно.
- в левой части – сумма арифметических квадратных корней, а в правой – отрицательное число – невозможно.
- Закрепление: решение иррациональных уравнений и систем
1) 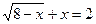
ОДЗ: 8-х≥0, х≤8, хÎ(-∞;8]
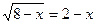
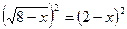
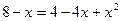
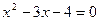
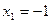
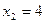
Проверка
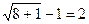 равенство верное
равенство верное 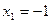 - корень
- корень
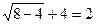 равенство неверное
равенство неверное 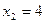 - посторонний корень
- посторонний корень
Ответ: 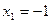
2) 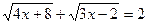
 ОДЗ:
ОДЗ:
 4x+8≥0 4x ≥-8 x≥-2
4x+8≥0 4x ≥-8 x≥-2
3х-2≥0 3х ≥ 2 х≥2/3 хÎ[2/3;∞)
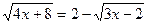
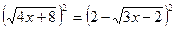
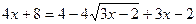
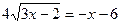
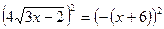
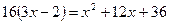
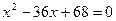
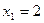
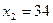
Проверка:
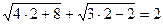 равенство неверное
равенство неверное 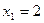 - посторонний корень
- посторонний корень
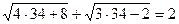 равенство неверное
равенство неверное 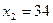 - посторонний корень
- посторонний корень
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|