Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

При решении задач с монетами число всех возможных исходов можно посчитать по формуле  п=2ª, где α –количество бросков

 При решении задач с монетами число всех возможных исходов можно посчитать по формуле  п=2ª, где α –количество бросков

19.  В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют 2 раза. Най­ди­те ве­ро­ят­ность того, что орел вы­па­дет ровно 1 раз.

Ре­ше­ние. Всего воз­мож­ны че­ты­ре ис­хо­да: решка-решка, решка-орёл, орёл-решка, орёл-орёл. Орёл вы­па­да­ет ровно один раз в двух слу­ча­ях, по­это­му ве­ро­ят­ность того, что орёл вы­па­дет ровно один раз равна 2:4=0,5. Ответ: 0,5.

20. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу. Ответ: 1:4=0,25

21. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл не выпадет ни разу.  Решение. 1:8=0,125  Ответ. 0,125                                                                               

22. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно 2 раза.                                                                          Решение. Составим список возможных вариантов. Бросают 2 раза может выпасть О - Орел, Р - Решка:
ОО, ОР, РО, РР. Всего 4 исхода из них только один случай удовлетворяет условию.   Вероятность (P) = 1 / 4 = 0.25. Ответ: 0.25

23. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что решка не выпадет ни разу.                                                                            Решение. Всего исходов 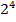 = 16, благоприятных  1 ( ОООО). 1:16 = 0,0625. Ответ: 0,0625                                                                               

При решении задач с кубиками число всех возможныхисходов можно посчитать по формуле  п=6ª, где α –количество бросков

24. Опре­де­ли­те ве­ро­ят­ность того, что при бро­са­нии иг­раль­но­го ку­би­ка (пра­виль­ной кости) вы­па­дет не­чет­ное число очков.                                                                                                     Ре­ше­ние.При бро­са­нии ку­би­ка рав­но­воз­мож­ных  шесть раз­лич­ных ис­хо­дов. Со­бы­тию "вы­па­дет нечётное число очков" удо­вле­тво­ря­ют три слу­чая: когда на ку­би­ке вы­па­да­ет 1, 3 или 5 очков. По­это­му ве­ро­ят­ность того, что на ку­би­ке вы­па­дет нечётное число очков равна 3:6=0,5. Ответ: 0,5.