
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача 1. Решить задачу 2. Задача 3
Задача 1
В основании прямой призмы лежит ромб с острым углом 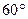 и стороной 8 см. Найдите меньшую диагональ призмы, если ее боковое ребро равно 6 см.
и стороной 8 см. Найдите меньшую диагональ призмы, если ее боковое ребро равно 6 см.
Решение:
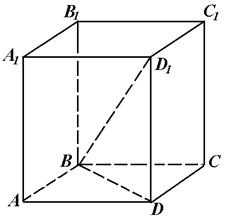
 – прямая призма. Ее основания
– прямая призма. Ее основания  – ромбы и
– ромбы и 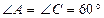 ,
,
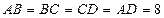 см. Ее высотой является боковое ребро,
см. Ее высотой является боковое ребро, 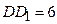 см. Тогда в
см. Тогда в 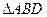
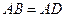 и
и 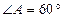 . Значит,
. Значит, 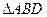 – равносторонний и
– равносторонний и 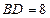 см. Так как
см. Так как 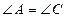 – острые углы ромба, то
– острые углы ромба, то 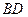 – его меньшая диагональ. Так как призма прямая, то
– его меньшая диагональ. Так как призма прямая, то 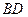 является проекцией меньшей диагонали призмы
является проекцией меньшей диагонали призмы 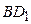 на ее основание.
на ее основание.
Из 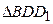 (
( 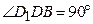 ):
):
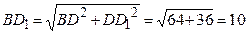 (см).
(см).
Ответ:10 см.
Решить задачу 2
В основании прямой призмы лежит ромб с острым углом 60о и стороной 6 см. Найдите меньшую диагональ призмы, если ее боковое ребро равно 8 см.
Задача 3
Высота правильной четырехугольной пирамиды4 см. Найдите площадь боковой поверхности пирамиды, если двугранный угол при основании равен 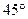 .
.
Решение:
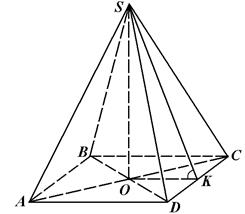
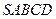 – правильная пирамида. Ее основание
– правильная пирамида. Ее основание 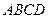 – квадрат.
– квадрат. 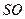 – ее высота,
– ее высота, 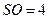 см и точка О является центром квадрата
см и точка О является центром квадрата 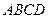 , то есть точкой пересечения его диагоналей. Проведем в плоскости основания
, то есть точкой пересечения его диагоналей. Проведем в плоскости основания 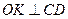 . Так как
. Так как 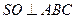 , то
, то 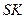 – наклонная к плоскости основания,
– наклонная к плоскости основания, 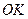 – проекция
– проекция 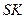 на плоскость основания и по теореме о трех перпендикулярах
на плоскость основания и по теореме о трех перпендикулярах 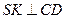 . Тогда
. Тогда 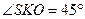 как линейный угол двугранного угла при основании пирамиды.
как линейный угол двугранного угла при основании пирамиды.
Площадь боковой поверхности найдем по формуле
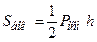 , где
, где
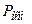 – периметр основания пирамиды,
– периметр основания пирамиды, 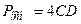 ;
;
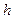 – апофема,
– апофема, 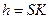 .
.
Так как 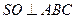 , то
, то 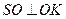 .
.
Из 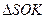
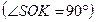 :
:
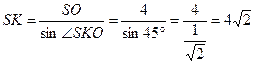 (см),
(см),
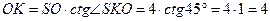 (см).
(см).
Так как точка О – центр квадрата 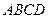 и
и 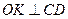 , то
, то 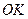 – радиус вписанной в основание окружности. Тогда
– радиус вписанной в основание окружности. Тогда 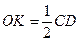 , а
, а 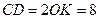 см и
см и 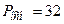 см.
см.
Тогда 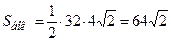 (см2).
(см2).
Ответ: 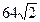 см2.
см2.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|