Контакты

Случайная статья

Для того чтобы определённый интеграл существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

⇐ ПредыдущаяСтр 2 из 2

Для того чтобы определённый интеграл существовал, достаточно чтобы подынтегральная функция была непрерывной на отрезке интегрирования.

Поэтому перед тем, как приступить к решению любого определённого интеграла, нужно убедиться в том, что подынтегральная функция непрерывна на отрезке интегрирования.

Определённый интеграл может быть равен отрицательному числу или нулю.

Нижний предел интегрирования может быть больше верхнего предела интегрирования.

ПРИМЕР:

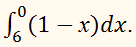
Интеграл вычисляется по формуле Ньютона-Лейбница.

Свойства определённого интеграла.

1) В определённом интеграле можно переставить верхний и нижний предел, сменив при этом знак.

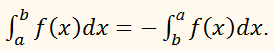
ПРИМЕР:

В определённом интеграле

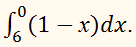
перед интегрированием целесообразно поменять пределы интегрирования на <<привычный>> порядок:

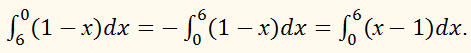
В таком виде интегрировать значительно удобнее.

2) Свойства линейности.

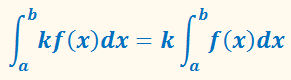
где k = const.

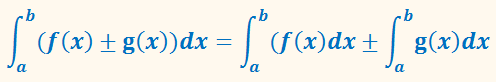
Это справедливо не только для двух, но и для любого количества функций.

ПРИМЕР:

Вычислить определённый интеграл:

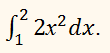
РЕШЕНИЕ:

Выносим константу за знак интеграла:

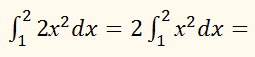
Интегрируем по таблице с помощью формулы

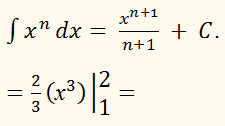
Используем формулу Ньютона-Лейбница.

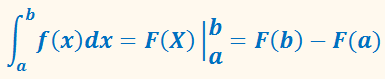
Сначала подставляем в х³ верхний предел, зптем нижний предел. Проводим дальнейшие вычисления и получаем окончательный ответ.

= ²/₃ (2³ – 1³) = ²/₃ (8 – 1) = ²/₃ ∙ 7 = ¹⁴/₃ = 4²/₃

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.