Выполнить упражнения на закрепление и самостоятельную работу.

Стр 1 из 2Следующая ⇒

Задание к уроку

1. По информационной карте к уроку изучить материал и ответить на вопросы:

1) Какая функция называется обратимой?

2) Какая функция называется обратной данной?

3) Как связаны область определения и множество значений функции и обратной ей функции?

4) Если функция задана аналитически, как задать формулой обратную функцию?

5) Если функция задана графически, как построить график обратной ей функции?

2. Выполнить упражнения на закрепление и самостоятельную работу.

Информационная карта к уроку

Тема: «Обратные функции. Область определения и область значений обратной функции. График обратной функции»

Рассмотреть график функции и перечислить изученные свойства функции.

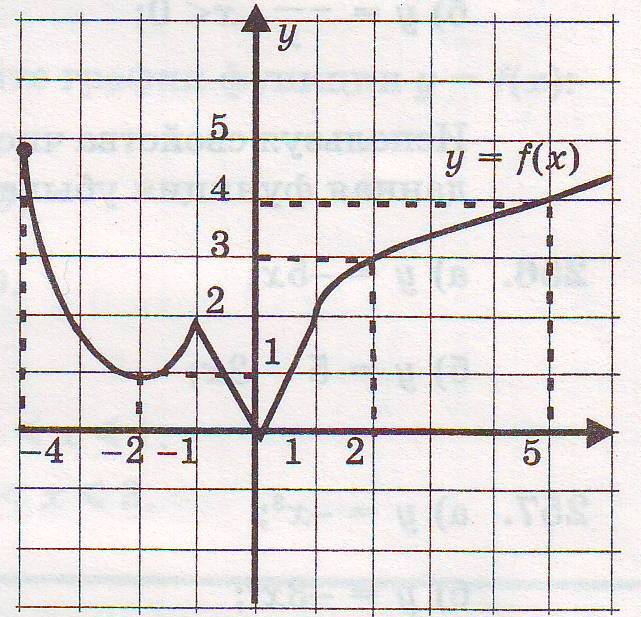
Определение 1: Функцию y=f(x) называют обратимой, если любое свое значение она принимает только в одной точке множества X.

Теорема: Если функция y=f(x)монотонна на множестве X , то она обратима.

Какая из предложенных функций обратима?

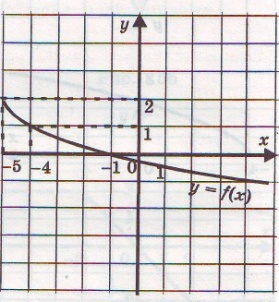
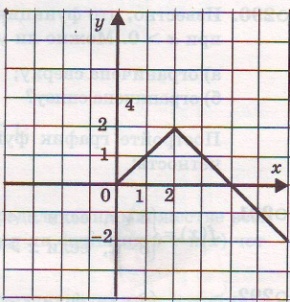
А) Б)

Определение 2: Пусть обратимая функция y=f(x) определена на множестве Х и Е(f)=Y. Поставим в соответствие каждому y из Y то единственное значение х, при котором

f(x)=y. Тогда получим функцию, которая определена на Y, а Х – область значений функции

Эту функцию обозначают x=f ^-1(y) и называют обратной по отношению к функции y=f(x).

Сделайте вывод о связи между областью определения и множеством значений обратных функций.

Замечание: монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием. Например, мы можем взять немонотонную функцию и рассмотреть ее только на одном промежутке, где она только возрастает или только убывает, тогда условие обратимости будет выполняться.

12 Следующая ⇒