Практическое занятие №29 Планетарные передачи

Практическое занятие №29 Планетарные передачи

Планетарная передача (ПП) — механическая передача вращательного движения, за счёт своей конструкции способная в пределах одной геометрической оси вращения изменять, складывать и раскладывать подводимые угловые скорости и/или крутящий момент. Обычно является элементом трансмиссии различных технологических и транспортных машин.

Конструктивно ПП всегда представляет собой набор взаимозацепленных зубчатых колёс (не менее 4), часть из которых (не менее 2) имеет общую геометрическую неподвижную ось вращения, а другая часть (также, не менее 2) имеет подвижные оси вращения, концентрически вращающиеся на так называемом «водиле» вокруг неподвижной. Зубчатые колёса на неподвижной оси всегда связаны друг с другом не напрямую , а через зубчатые колёса на подвижных осях, а ввиду того, что вторые способны не только вращаться относительно первых, но и обкатывать их, тем самым передавая поступательное движение на водило, все звенья ПП, на которые можно подавать/снимать мощность, получают возможность вращаться дифференциально, с тем лишь условием, что угловая скорость любого такого звена не абсолютно хаотична, а определяется угловыми скоростями всех остальных звеньев. В этом плане ПП похожа на планетарную систему, в которой скорость каждой планеты определяется скоростями всех остальных планет системы. Дифференциальный принцип вращения всей системы , а также то, что в своём каноническом виде набор зубчатых колёс, составляющих ПП, собран в некоем подобии солнца и эпициклически движущихся по орбите планет, даёт данной механической передаче такие присущие только ей интернациональные определения, как планетарная, дифференциальная (от лат. differentia — разность, различие) или эпициклическая, каждое из которых в данном случае есть синонимы.

С точки зрения теоретической механики планетарная передача — это механическая система с двумя и более степенями свободы. Эта особенность, являющаяся прямым следствием конструкции, есть важное отличие ПП от каких-либо других передач вращательного движения, всегда имеющих только одну степень свободы. И эта особенность наделяет саму ПП тем важным качеством, что в аспекте воздействия на угловые скорости вращения ПП может не только редуцировать эти скорости , но и складывать и раскладывать их, что, в свою очередь, делает её основным механическим исполнительным узлом не только различных планетарных редукторов, но таких устройств, как дифференциалы и суммирующие ПП.

Планетарная передача с остановленным водилом по сути является двухступенчатой зубчатой передачей с неподвижными осями колес.

Планетарная передача и планетарный механизм[править | править код]

В русскоязычной инженерной терминологии термины планетарная передача (далее — ПП) и планетарный механизм (далее — ПМ) зачастую предполагаются как синонимы. Отличия в том, что термин ПП обычно используется в контексте принципиального понимания устройства той или иной передачи вращательного движения, особенно если устройство такой передачи не очевидно (скрыто корпусом/картером) или такая передача обладает определёнными уникальными свойствами, присущими только планетарной, и на этом надо акцентировать внимание. А термин ПМ используется для обозначения конкретного зубчато-рычажного механизма, причём существуют критерии, позволяющие чётко описать ПМ как сборочный узел в составе более крупного узла или агрегата и определить, сколько и каких именно использовано ПМ в конкретной передаче вращательного движения.

Состав планетарного механизма[править | править код]

Конструкция ПП/ПМ основана на различных комбинациях из трёх основных и нескольких одинаковых вспомогательных звеньев. Три основные звена с одной общей осью вращения — два центральных зубчатых колеса и водило. Вспомогательные звенья — набор одинаковых зубчатых колёс на подвижных осях вращения и подшипники.

· Малое центральное зубчатое колесо с внешними зубьями называется солнечной шестернёй или солнцем (С).

· Большое центральное зубчатое колесо с внутренними зубьями называется коронной, эпициклической шестернёй или эпициклом (Э).

· Водило (В) является основой ПМ — это неотъемлемая деталь абсолютно любого ПМ и краеугольный камень всей идеи передачи вращения через планетарную систему с дифференциальной связью. Водило представляет собой рычажный механизм — обычно такую пространственную вилку, ось «основания» которой совпадает с осью самого ПМ, а оси «зубцов» с установленными на них сателлитами концентрически вращаются вокруг неё в плоскости/плоскостях расположения центральных зубчатых колёс. Оси «зубцов» — это и есть так называемые подвижные оси или оси сателлитов

· Сателлиты (Ш) представляют собой зубчатые колёса (или группы колёс) с внешними зубьями. При этом сателлиты находятся в одновременном и постоянном зацеплении с обоими центральными зубчатыми колёсами ПМ. Количество сателлитов в ПМ обычно составляет от двух до шести (чаще всего — три, так как только при трёх сателлитах нет нужды в специальных уравновешивающих механизмах) и точного значения для функциональности ПМ не имеет. В различных ПМ применяются сателлиты одновенцовые (одно простое зубчатое колесо), двухвенцовые (два соосных зубчатых колеса с общей ступицей), трёхвенцовые и так далее. Также сателлиты могут быть парными — то есть, располагающимися на осях одного водила и зацепленными в паре.

Зубчатые колёса, составляющие ПМ, могут быть любого известного типа: прямозубые, косозубые, шевронные, червячные. Тип зацепления в общем случае не важен и на принципиальную работу ПП влияния не оказывает.

В любом ПМ оси вращения центральных зубчатых колёс и водила всегда совпадают. Однако это не значит, что оси сателлитов всегда будут параллельны основной оси. Как и в случае с простыми зубчатыми передачами, здесь возможны варианты параллельных, скрещивающихся и пересекающихся осей. Пример второго варианта — межколёсный дифференциал с коническими зубчатыми колёсами. Пример третьего варианта — самоблокирующийся дифференциал Torsen с червячным зацеплением.

Любой ПМ, независимо простой он или сложный, плоский или пространственный, для своей работоспособности должен иметь одно водило с сателлитами и не менее двух любых центральных зубчатых колёс. Под определением «два любые» подразумевается, что это могут быть не только одно солнце и один эпицикл, но и два солнца и ни одного эпицикла, или два эпицикла и ни одного солнца. Три звена, в том числе водило, есть необходимое и достаточное условие для того, чтобы ПМ мог выполнять функции передачи мощности и сложения/разложения потоков: работать в качестве редуктора (в том числе многоскоростного), в качестве дифференциала или суммирующей ПП. Также три звена есть основа такого русскоязычного технического термина, как Трёхзвенный Дифференциальный Механизм (или ТДМ).

Формально, механизмы, состоящие всего из двух звеньев — из водила и всего лишь одного центрального зубчатого колеса — также могут именоваться планетарными. Фактически же, такие двухзвенные ПМ трудно разумно приспособить для выполнения какой-либо работы: они не годятся для передачи мощности с одного основного звена на другое и лишь при определённых условиях могут работать как переусложнённая прямая передача. Увеличение числа основных звеньев одного ПМ в большую сторону — до 4 и более — возможно и формально и фактически, однако при этом такие ПМ не приобретают никаких новых свойств, хотя и получают больше теоретически доступных передаточных отношений и могут давать проектируемой ПП определённые компоновочные преимущества.

Простые и сложные ПМ, планетарный ряд[править | править код]

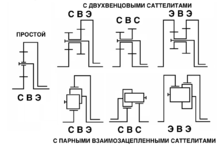
Простые ПМ

Схемы наиболее распространённых сложных планетарных механизмов

Критерием деления ПМ на простые и сложные является число составляющих его основных звеньев (именно основных, а число сателлитов — не в счёт) . Простой ПМ имеет всего три основных звена: одно водило и два любых центральных зубчатых колеса. Кинематика допускает всего-лишь 7 (семь!) ПМ , подпадающих под это условие: один наиболее распространённый и всем известный, так называемый «элементарный», с набором одновенцовых сателлитов схемы СВЭ; три ПМ с двухвенцовыми саттелитами (СВЭ, СВС, ЭВЭ) и три ПМ с парными взаимозацепленными сателлитами (СВЭ, СВС, ЭВЭ)).

Сложных ПМ гораздо больше чем простых. Их точное число не определено ввиду отсутствия такой нужды, а наиболее распространённые из них приведены на рисунке. Точно так же как и простые ПМ, сложные имеют всего одно водило, но центральных зубчатых колёс может быть три и более. При этом в составе сложного ПМ всегда умозрительно можно выделить несколько простых ПМ (конкретно: три в четырёхзвенном и шесть в пятизвенном) , каждый из которых в себя включает два каких-то центральных зубчатых колеса и одно общее водило.

Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой ПМ с набором одновенцовых сателлитов является однорядным. Все три простые ПМ с двухвенцовыми сателлитами — двухрядные. ПМ с парными взаимозацепленными сателлитами схемы СВЭ — однорядный ; схем СВС и ЭВЭ — двухрядные. Таким образом, все простые ПМ могут быть или однорядными или двухрядными. Сложные ПМ, в свою очередь, могут быть двух, трёх и четырёхрядные. Верхнее число рядов в сложном ПМ формально не ограничено, хотя фактически уже пятирядные есть большая редкость, хотя в сборках из планетарных механизмов, применяющихся в многоступенчатых планетарных коробках передач, общее число рядов может быть пять и больше. Нередко термины ПМ и планетарный ряд предполагаются как синонимы, но, в общем случае, это неверно: даже если в отдельных случаях оба термина могут обозначать одно и то же, всегда следует помнить, что их смысл несколько разный.

Плоские и пространственные ПМ[править | править код]

Свободный дифференциал на основе простого плоского двухрядного ПМ с парными сателлитами

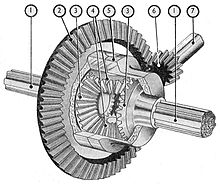
Свободный дифференциал на основе пространственного ПМ с коническими шестернями

Наличие в составе одного ПМ более одного планетарного ряда не означает, что он является пространственным. Сколько бы ни было рядов, но если плоскости вращения всех составляющих каждый ряд зубчатых колёс параллельны, то такой ПМ будет оставаться плоским. Критерием отличия плоского ПМ от пространственного является наличие не просто более одной плоскости вращения составляющих его зубчатых колёс, но наличие непараллельных плоскостей их вращения. Плоскости вращения звеньев в пространственном ПМ не обязаны быть строго перпендикулярны друг-другу и могут находиться под любыми произвольными углами. Примером пространственного ПМ может служить конический симметричный дифференциал, наподобие применяющегося в приводе ведущих колёс автомобиля. А вот близкий по конструкции цилиндрический дифференциал, применяющийся там же и выполняющий точно такие же функции, будет оставаться плоским ПМ.

Пространственные ПМ по своему функционалу ничем не отличаются от аналогичных по составу плоских ПМ. Выбор того или иного ПМ в качестве основы конкретной ПП есть лишь вопрос экономики или конструкторских предпочтений. Тот же простой межколёсный дифференциал почти всегда выполнен на основе пространственного ПМ не потому, что что плоский не годится, а, скорее, по определённым компоновочным соображениям. Плюс, как это ни странно, пространственный ПМ для выполнения схожих функций может требовать меньшего количества шестерён и деталей вообще. Так, тот же межколёсный дифференциал в пространственном варианте требует всего лишь 4 одинаковые шестерни, из которых две пойдут на два солнца и две — на два саттелита. В случае же плоского варианта, таких шестерён потребуется как минимум шесть, а скорее всего — восемь, и при этом они обязательно будут двух разных типоразмеров.

2 степени свободы ПМ[править | править код]

Уникальной особенностью любого ПМ, отличающей его от всех прочих зубчатых передач, является наличие у него двух степеней свободы. Применительно к простому трёхзвенному ПМ это означает, что понимание угловой скорости вращения любого одного основного звена не даёт однозначного понимания угловых скоростей двух других основных звеньев, даже если известны все передаточные отношения внутри ПМ. Здесь все три основных звена находятся в дифференциальной связи друг с другом и для определения их угловых скоростей надо знать угловые скорости как минимум двух из них. В этом есть важное отличие ПМ от прочих зубчатых механизмов, в которых угловые скорости всех элементов связаны линейной зависимостью, а по угловой скорости одного элемента всегда можно точно определить угловые скорости всех остальных элементов, сколь много их бы не было. И в этом есть основа уникальных свойств, присущих любому ПМ: способность изменять угловые скорости на выходе при неизменных угловых скоростях на входе, способность делить и суммировать потоки мощности и всё это при постоянно зацепленных шестернях.

Любой ПМ, независимо от того, простой он или сложный, имеет фактически лишь две степени свободы. Для простого ПМ это подтверждается и визуальным наблюдением за работой такого механизма и уравнением Чёбышева. Для сложных ПМ это визуально не очевидно, а уравнение Чёбышева теоретически может допускать существование для таких ПМ трёх степеней свобод, что подразумевает наличие четырёх звеньев, находящихся в дифференциальной связи друг с другом. Но фактически такие сложные ПМ будут физически неработоспособны в тех практических задачах, ради которых они создаются, а все работоспособные сложные ПМ останутся двухстепенными. Независимо от числа основных звеньев любого работоспособного сложного ПМ, в нём, так же как и в простом ПМ, в дифференциальной связи друг с другом будет находиться только три основных звена, а остальные основные звенья, сколько бы их ни было, будут иметь линейную связь с каким-то одним из трёх вышеупомянутых. Попытки же создания сложных ПМ с тремя (и тем более, с четырьмя) фактическими степенями свободы считаются бесперспективными, а все работоспособные трёх- и четырёхстепенные ПП основаны на сборке последовательно взаимозацепленных двухстепенных ПМ.

Передаточное отношение[править | править код]

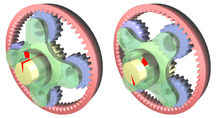
Планетарная передача в режиме повышения скорости. Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.

Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение различными способами.

При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, а два других служат в качестве ведущего и ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также от того, какой элемент закреплён.

Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как {\displaystyle S}, а для планетарных шестерён примем это число как {\displaystyle P}, то передаточное отношение будет определяться формулой {\displaystyle {\frac {S}{P}}}, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет {\displaystyle -{\frac {24}{16}}}, или {\displaystyle -{\frac {3}{2}}}, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.

Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет {\displaystyle A} зубьев, то оно будет вращаться с соотношением {\displaystyle {\frac {P}{A}}} относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно {\displaystyle {\frac {16}{64}}}, или {\displaystyle {\frac {1}{4}}}. Таким образом, объединив оба примера, мы получим следующее:

· Один оборот солнечной шестерни даёт {\displaystyle -{\frac {S}{P}}} оборотов планетарных шестерён;

· Один оборот планетарной шестерни даёт {\displaystyle {\frac {P}{A}}} оборотов кольцевой.

В итоге, если водило заблокировано, общее передаточное отношение системы будет равно {\displaystyle -{\frac {S}{A}}}.

В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет меньше единицы и составит {\displaystyle {\frac {1}{(1+{\frac {A}{S}})}}}.

Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно {\displaystyle 1+{\frac {A}{S}}}. Это самое большое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.

Всё вышесказанное можно описать следующими двумя уравнениями (выведены из условия отсутствия проскальзывания сопрягаемых шестерён и следовательно равенства дуг, проходимых точками, находящихся на окружностях, в единицу времени):

{\displaystyle {\begin{aligned}A\left(\omega _{a}-\omega _{c}\right)=P\omega _{p}\\S\left(\omega _{s}-\omega _{c}\right)=-P\omega _{p}\end{aligned}}}

Здесь {\displaystyle \omega _{a},\omega _{c},\omega _{p},\omega _{s}} — угловые скорости соответственно: кольцевой шестерни, водила, планетарных шестерён относительно водила, и солнечной шестерни. Первое уравнение характеризует вращение водила относительно кольцевой шестерни, второе — солнечной шестерни относительно водила.

Если исключить из уравнений {\displaystyle \omega _{p}} путём их сложения — получится одно уравнение: {\displaystyle A\omega _{a}+S\omega _{s}=(A+S)\omega _{c}}. Так как числа зубьев шестерён всегда удовлетворяют условию {\displaystyle A=S+2P} (исходя из простых геометрических соотношений, поскольку в диаметр коронной шестерни помещается диаметр солнечной шестерни и два диаметра сателлитов), по-другому это уравнение можно записать как:

{\displaystyle \left(2+n\right)\omega _{a}+n\omega _{s}-2\left(1+n\right)\omega _{c}=0}

Где n — это параметр передачи, равный {\displaystyle n={S \over P}}, то есть отношению чисел зубьев солнечной и планетарных шестерён.

Описание элементов для следующей таблицы^[1]
Название	Количество зубцов	Обороты
{\displaystyle {\color {blue}Driving}}	{\displaystyle {\color {blue}z}}	{\displaystyle {\color {blue}n}}
{\displaystyle {\color {magenta}Auxiliary\ driving}}	{\displaystyle {\color {magenta}z}}	{\displaystyle {\color {magenta}n}}
{\displaystyle {\color {red}Driven}}	{\displaystyle {\color {red}z}}	{\displaystyle {\color {red}n}}
{\displaystyle Fixed}	{\displaystyle z}	{\displaystyle n}
{\displaystyle {\color {green}Planetary}}	{\displaystyle {\color {green}z}}	{\displaystyle {\color {green}n}}
{\displaystyle {\color {cyan}Planetary}}	{\displaystyle {\color {cyan}z}}	{\displaystyle {\color {cyan}n}}

В нижеуказанной таблице (указывающей выходные скорости различных типов планетарных передач в зависимости от их конструктивных особенностей) приняты следующие условные обозначения:

· синим цветом обозначено ведущее звено, этим же цветом указано количество зубьев {\displaystyle z} и угловая скорость {\displaystyle n} этого звена в формуле;

· пурпурным цветом обозначено вспомогательное звено, этим же цветом указано количество зубьев {\displaystyle z} и угловая скорость {\displaystyle n} этого звена в формуле;

· чёрным цветом обозначено неподвижное (зафиксированное) звено, этим же цветом указано количество зубьев {\displaystyle z} этого звена в формуле;

· зелёным цветом обозначено планетарное звено {\displaystyle 1}, этим же цветом указано количество зубьев {\displaystyle z} и угловая скорость {\displaystyle n} этого звена в формуле;

· голубым цветом обозначено планетарное звено {\displaystyle 2}, этим же цветом указано количество зубьев {\displaystyle z} и угловая скорость {\displaystyle n} этого звена в формуле.

12 Следующая ⇒