Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки

Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки

экстремума. Графическая интерпретация

Промежутки монотонности функции:

Промежутки монотонности – это промежутки оси x, на которых функция возрастает (промежутки возрастания) или убывает (промежутки убывания).

Геометрически – это интервалы оси x, где график функции идет вверх или вниз.

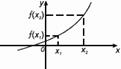Определение. Функция f(x) называется возрастающей, если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁)< f(x₂).

Из этого определения следует, что для любых двух точек правая точка лежит выше левой.

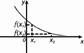
Определение. Функция f(x) называется неубывающей, если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁)≤ f(x₂).

Из этого определения следует, что для любых двух точек правая точка лежит не ниже левой.

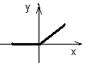
Определение. Функция f(x) называется убывающей, если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁) > f(x₂).

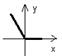
Определение. Функция f(x) называется невозрастающей, если для любых x₁ и x₂ из этого множества, таких, что x₁ < x₂ выполнено неравенство f(x₁) ≥ f(x₂).

Определение. Функция называется строго монотонной, если она возрастающая или убывающая.

Определение. Функция называется монотонной, если она неубывающая или невозрастающая

Существуют функции, которые не удовлетворяют определениям. Например, функция у=х², на интервале (-8;0) – она убывающая, на интервале (0;+8) она возрастающая. Это пример кусочно-монотонной функции.

Определение. Функция называется кусочно-монотонной, если любой интервал, принадлежащий области определения моно разбить на конечное или бесконечное число интервалов, в каждом из которых эта функция монотонна.

⇐ Предыдущая 123 Следующая ⇒