Контакты

Случайная статья

Пример 1.

Стр 1 из 2Следующая ⇒

Лекция 6.«Способы решения показательных уравнений и систем уравнений»

Показательным называется уравнение, в котором переменная входит только в показатели степеней, при заданном основании.

Уравнения вида 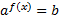, 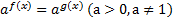называются простейшими показательными уравнениями.

В самом простом случае уравнение принимает вид: .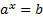

Так как множество значений показательной функции 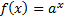- множество положительных чисел, то при уравнение решений не имеет.

Теперь рассмотрим случай b>0.

Вспомним, что показательная функция при a>1 монотонно возрастает и принимает все положительные значения, каждое ровно один раз. В случае 0<a<1 показательная функция монотонно убывает и также принимает все положительные значения, каждое ровно один раз.

Для того чтобы решить простейшее показательное уравнение 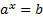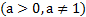, нужно число b представить в виде степени числа a.

Рассмотрим пример: .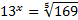

Представим 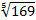в виде степени числа 13: .

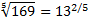Теперь перепишем данное уравнение в виде: , поэтому x=2/5.

Ответ: x=2/5.

Теперь перейдем к решению более сложных показательных уравнений.

1. Рассмотрим уравнение вида:

.

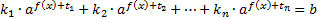То есть мы видим, что левая часть этого уравнения представляет собой сумму, слагаемые которого отличаются коэффициентами 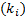и показатели степеней с одинаковыми основаниям отличаются слагаемыми .

Для решения таких уравнений левую часть преобразуют следующим образом: выносят за скобку степень 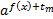(часто, чтобы избежать дробных коэффициентов, выносят степень с наименьшим показателем):

Мы видим, что выражение в скобках представляет собой число.

Поэтому выразим 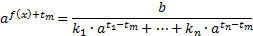и решим простейшее показательное уравнение.

Рассмотрим пример:

.

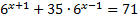Решение:

Преобразуем левую часть и вынесем за скобку :

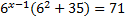
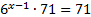
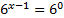
x-1=0

x=1

Ответ: x=1.

2. Рассмотрим еще одно уравнение, которое решается с помощью вынесения за скобку общего множителя.

.

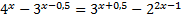Решение:

Преобразуем уравнение: перенесем степени с одинаковыми основаниями в одну часть:

,

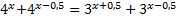Вынесем за скобку множители с одинаковыми показателями:

, .

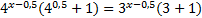Теперь преобразуем полученное уравнение к виду: 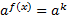. Для этого разделим обе части уравнения на 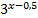и на 3:

.

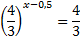x-0,5=1

x=1,5.

Ответ: x=1,5.

3. Еще один вид показательных уравнений – уравнения, сводящиеся к квадратным:

.

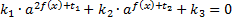В этом случае вводят новую переменную: 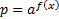. Получим вспомогательное уравнение: .

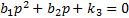После решения этого уравнения получим простейшие показательные уравнения.

Рассмотрим пример:

.

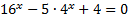Решение:

Введем новую переменную: .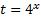

Запишем вспомогательное уравнение: .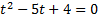

. Вернемся к переменной х:

, .

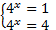Ответ:

4. Еще один вид уравнений, который сведется к решению квадратного или уравнения третей степени, это однородное уравнение.

Однородным показательным уравнением называется уравнение вида:

Здесь f и g функции вида: 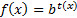, 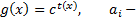коэффициенты.

Однородные показательные уравнения решаются делением на 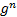или на 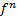и последующей заменой: .

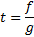Рассмотрим пример:

.

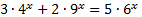Решение:

Заметим, что 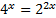, , 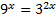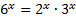. То есть уравнение можно записать в виде:

.

Разделим уравнение на 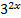, получим уравнение: 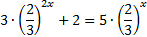. Теперь введем новую переменную: 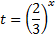и получим вспомогательное уравнение:

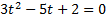, решим его:

.

, .

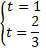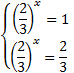Ответ: .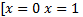

Пример 1.

Решите уравнение: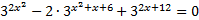

Решение: Запишем уравнение в виде:

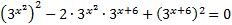
Таким образом, уравнение является однородным относительно функци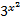й: и .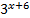

Разделим уравнение на 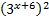и получим:

.

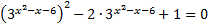Введем новую переменную: .

Вспомогательное уравнение:

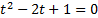
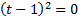
Вернемся к исходной переменной:

.

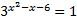
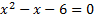
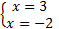Ответ: .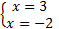

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.