Лабораторная работа №4. I. Теоретическая часть

Лабораторная работа №4

«Вычисления с исключением ошибок округления с рациональными числами по одному модулю»

Целью данной лабораторной работы является изучение работы с вычислениями с исключением ошибок округления с рациональными числами в модулярной арифметики по одному модулю.

I. Теоретическая часть

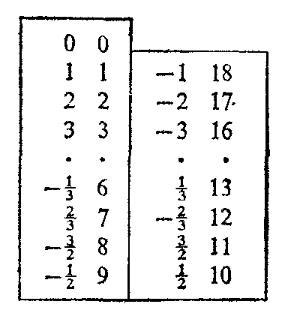
Пример таблицы представления дробей Фарея 3-го порядка по модулю 19 представлен в таблице 1.

Многоточие в таблице на месте чисел 4,5 и других означает, что эти числа не являются дробями Фарея 3-го порядка и согласно теореме не имеют единственного представления.

Таблица 1. Представление дробей Фарея 3-го порядка

Таким образом, если все исходные данные и решения некоторой вычислительной задачи содержатся во множестве дробей Фарея порядка N, то возможно применение вычислений с исключением ошибок округления следующим образом:

1. Перевести операнды из Fn во множество целых чисел по модулю p

2. Выполнить все арифметические в модулярной арифметики по модулю р

3. Выполнит обратное преобразование из модулярной системы счисления в дроби Фарея

Эти действия показаны на рисунке 1 в виде схемы вычислений с исключением ошибок округления.

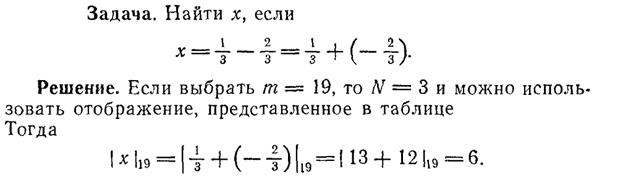
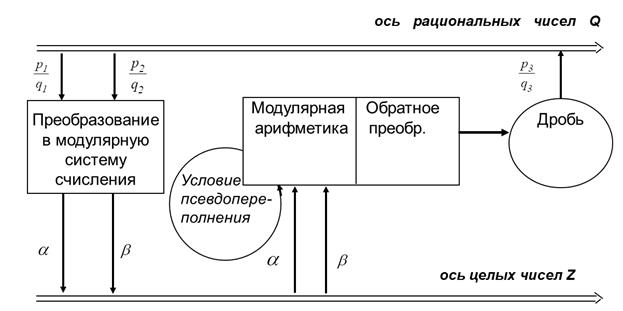
Рисунок 1. Вычисления с исключением ошибок округления по одному модулю

Прямое и обратное преобразование дробей в модулярную арифметику.

1. Прямое преобразование дроби x/y в модулярную систему счисления по модулю m.

x/y = x ∙ y^-1 по определению и задача прямого преобразования сводится к задаче нахождения обратного к y по модулю p

Пример нахождения обратного приведен ниже:

2. Обратное преобразование из модулярной системы счисления по модулю р в дробь Фарея (метод Корнерупа, Кришнамурти)

12 Следующая ⇒