Условие для каждого задания и ответы должны быть обязательно!

Условие для каждого задания и ответы должны быть обязательно!

Вариант 3

1. Матрица линейного оператора поворота векторов на плоскости вокруг начала координат на угол α в базисе (i, j) имеет вид

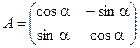Найти образ вектора 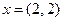, если 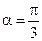. Сделать рисунок.

2. Проверьте свойства линейного оператора поворота, используя данные из условия задания 1 (для λ = –5).

3. Заданы векторы 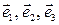в некотором базисе. Проверить, что векторы 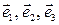составляют базис. Применяя процесс ортогонализации построить новый ортогональный базис.

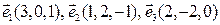Ответ выведите в формате rat.

4. Линейный оператор в базисе 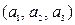задан матрицей А. Найти его матрицу в базисе 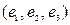, если известно разложение векторов 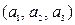по базису :

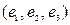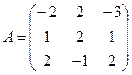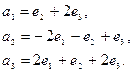
Ответ выведите в формате rat.

Результат отправляете на диск Common в папку вашей группы в формате:

№PC_Фамилия(на русском языке)_KR_09_03(номер варианта).docx.

Например,

03_Иванов_ KR_09_03.docx