Итоговая контрольная работа №3 (KR_03)

Итоговая контрольная работа №3 (KR_03)

Условие для каждого задания и ответы должны быть обязательно!

Вариант 1

Решите систему уравнений по правилу Крамера. Сделайте геометрическую иллюстрацию решения.

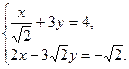
С помощью обратной матрицы решите систему уравнений из условия задачи 1. Сделайте проверку.
Даны векторы a, b, c. Проверьте, составляют ли они базис. В случае положительного ответа разложите по данному базису вектор d. При решении используйте правило Крамера или обратную матрицу. Сделайте проверку.

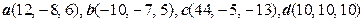Даны три точки А(1,2,0), В(3,2,1) и С(-2,1,2). Вычислите площадь треугольника АВС по известной формуле 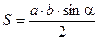. Результат проверьте с помощью свойства векторного произведения.
Используя свойство смешанного произведения, найдите объем пирамида ABCD, если A(7, 2, 4), В(7, -1, -2), С(3, 3, 1), D(-4, 2, 1).

Результат отправляете на диск Common в папку вашей группы в формате:

№PC_Фамилия(на русском языке)_KR_03_01(номер варианта).docx.

Например,

03_Иванов_ KR_03_01.docx

Условие для каждого задания и ответы должны быть обязательно!

Вариант 2

Решите систему уравнений по правилу Крамера. Сделайте геометрическую иллюстрацию решения.

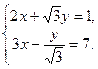
С помощью обратной матрицы решите систему уравнений из условия задачи 1. Сделайте проверку.
Даны векторы a, b, c. Проверьте, составляют ли они базис. В случае положительного ответа разложите по данному базису вектор d. При решении используйте правило Крамера или обратную матрицу. Сделайте проверку.

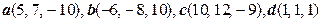Даны три точки А(1,-1,2), В(5,-6,2) и С(1,3,-1). Вычислите длину высоты, опущенной из вершины В на сторону АС и угол между векторами АВ и АС.
Используя свойство смешанного произведения, найдите объем пирамида ABCD, если A(1, 3, 6), В(2, 2, 1), С(-1, 0, 1), D(-4, 6, -3).

Результат отправляете на диск Common в папку вашей группы в формате:

№PC_Фамилия(на русском языке)_KR_03_02(номер варианта).docx.

Например,

03_Иванов_ KR_03_02.docx