
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теорема: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Теорема: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
| Анализ: | ||||||||||||
| Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. | Что нам дано? -прямая - не лежащая на ней точка Что нужно доказать? - проходит плоскость -и при том только одна! | |||||||||||
| Что мы знаем? – АКСИОМЫ!!!! | ||||||||||||
Дано:
a – прямая
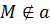 Док-во:
Док-во:
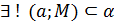
|
 
| |||||||||||
| Для доказательства теоремы нужно : 1). Существовует ли вообще такая плоскость 2). И если такая плоскость существует, то она единственная! | ||||||||||||
| А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и при том только одна | ||||||||||||
Док-во:
1. Существование:
1). Отметим две точки 
|

| |||||||||||
2). M, P,Q – не лежат на одной прямой( так как 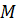 не принадлежит прямой не принадлежит прямой  ( ( 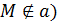 , а P,Q принадлежат( , а P,Q принадлежат( 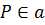 , , 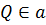 ) )
| ||||||||||||
3). Что я знаю? - АКСИОМЫ
По А1проведем плоскость 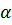
| ||||||||||||
| Мы доказали, что плоскость существует! Теперь нужно доказать, что она ЕДИНСТВЕННАЯ! | ||||||||||||
Какую бы плоскость мы не взяль – любая будет проходить четез точки M, P,Q 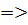 она совпадет с она совпадет с 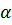
| ||||||||||||
| Так как по А1 через M, P,Q проходить только одна плоскость | ||||||||||||
Теорема: Через две пересекающиеся прямые проходит плоскость, и притом только одна.
| Анализ: | |||
| Через две пересекающиеся прямые проходит плоскость, и притом только одна. | Что нам дано? -две пересекающиеся прямые Что нужно доказать? - проходит плоскость -и при том только одна! | ||
| Что мы знаем? – АКСИОМЫ!!!! | |||
Дано:
 Док-во:
Док-во:

| 
| ||
| Для доказательства теоремы нужно : 1). Существовует ли вообще такая плоскость 2). И если такая плоскость существует, то она единственная! | |||
Док-во:
1. Существование:
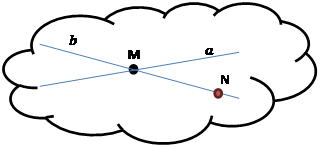
1) Отметим на прямой 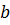 точку точку 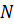 2)
2)
 и отмеченную точку и отмеченную точку 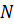 плоскость плоскость 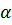
3) Две точки прямой |
| ||
Что мы знаем??? А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости | |||
Значит вся прямая 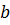 будет лежать в плоскости будет лежать в плоскости 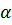 . Следовательно плоскость . Следовательно плоскость 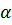 проходит через прямую проходит через прямую 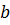
| |||
| 2. Единственность | |||
| Что мы знаем??? Т. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. | |||
| Следовательно из теоремы, через точку и прямую и точку проходит единственная плоскость | |||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
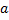


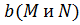 лежат в плоскости
лежат в плоскости 