Тема: Применение производной для отыскания наибольшего и наименьшего значения функций.

Образовательные: сформировать понятие о применении производной для нахождения наибольшего и наименьшего значения функции, непрерывной на отрезке; научить применять производную для нахождения наибольшего и наименьшего значения функции на отрезке и незамкнутом промежутке.

Развивающие: развитие логического мышления, памяти, внимания; развитие общеучебных умений, умения сравнивать и обобщать.

Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры.

Тип урока: совершенствование знаний, умений и навыков.

Оборудование:интерактивная доска, компьютер, проектор, дидактический материал, презентация.

Ход урока:

 «Математика — это доказательство самых очевидных вещей наименее очевидным способом»   Джоржд Пойа.

1. Организационный момент.(3 мин)

Анализ самостоятельной работы, проведенной на предыдущем уроке.

2. Повторение (фронтальный опрос).(7 мин)

1. Решить уравнения  устно:

1) ; ( )

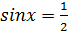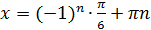2) ; ( )

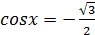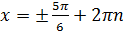3) 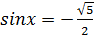; (решений нет)

2. Найти производную:

4) ;

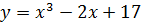5) ;

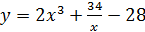6) ;

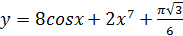3. Исследовать функцию.

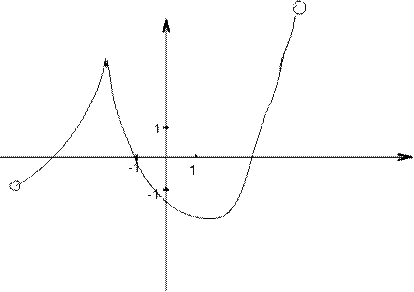
3. Актуализация знаний.(  мин)

Для того, чтобы вспомнить основной алгоритм вычисления наибольшего и наименьшего значения, я предлагаю вам выполнить ранжирование, то есть составить правильный порядок действий при данном вычислении.

1. Находим производную.

2. Приравниваем производную к нулю.

3. Решаем полученное уравнение.

4. Размещаем полученные стационарные и критические точки на числовой прямой.

5. Находим промежутки монотонности.

6. Вычисляем значение функции в критических или стационарных точках и на концах отрезка.

7. Записываем ответ.

Теперь закрепим этот алгоритм на практике. Задания на нахождение наибольшего и наименьшего значения в ЕГЭ 2016 расположены под номером 12. Прорешаем некоторые их типы.

4. Практические задания (15 мин)

1. Найти наибольшее значение функции 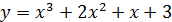 на промежутке .

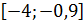2. Найти наименьшее значение функции 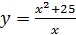на промежутке .

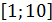3. Найти наибольшее значение функции 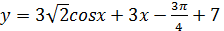на отрезке .

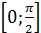4. Найти наименьшее значение функции 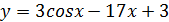 на отрезке .

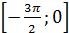5. Физкультминутка(2 мин)