Хелпикс

Главная

Контакты

Случайная статья



ЗАДАНИЯ № 6-11. ЗАДАНИЕ № 6. ЗАДАНИЕ № 7. ЗАДАНИЕ № 8. ЗАДАНИЕ № 9. ЗАДАНИЕ № 10. ЗАДАНИЕ № 11

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


ЗАДАНИЯ № 6-11

Ниже приведены несколько видов уравнения Шредингера для общего и частного случаев:

А) ;

Б) ;

В) ;

Г) ;

Д) ;

 E) .

ЗАДАНИЕ № 6

Общим уравнением Шредингера является…

 

 ВАРИАНТЫ ОТВЕТОВ:

1)  A;       2)  Б;       3)  В;       4) Г;       5)  Д;  6)  E.

ЗАДАНИЕ № 7

Уравнением Шредингера для стационарных состояний в общем случае является уравнение…

 

 ВАРИАНТЫ ОТВЕТОВ:

1) A;  2) Б;  3) В;  4) Г;  5) Д; 6) E.

ЗАДАНИЕ № 8

Уравнением Шредингера для электрона в водородоподобном атоме является уравнение…

 

 ВАРИАНТЫ ОТВЕТОВ:

1) A;  2) Б;  3) В;  4) Г;  5) Д; 6) E.

 

ЗАДАНИЕ № 9

Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение…

 

 ВАРИАНТЫ ОТВЕТОВ:

 1) A;  2) Б;  3) В;  4) Г;  5) Д; 6) E.

 

ЗАДАНИЕ № 10

Уравнением Шредингера для частицы в трехмерной прямоугольной “потенциальной яме” с бесконечными прямоугольными стенками является уравнение…

 

 ВАРИАНТЫ ОТВЕТОВ:

1) A;  2) Б;  3) В;  4) Г;  5) Д; 6) E.

ЗАДАНИЕ № 11

Уравнением Шредингера для частицы в одномерной прямоугольной “потенциальной яме” с бесконечными прямоугольными стенками является уравнение …

 

 ВАРИАНТЫ ОТВЕТОВ:

1) A;  2) Б;  3) В;  4) Г;  5) Д; 6) E.

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

Указание к заданиям 6 -11.

Общее уравнение Шредингера:

 ,

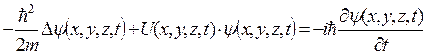где 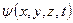 – волновая функция;

;

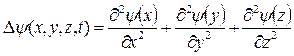m −масса частицы;

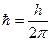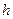(  − постоянная Планка);

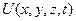 −  потенциальная энергия.

Для стационарного случая уравнение Шредингера:

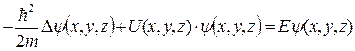   или

,

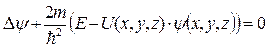где E –  энергия частицы.

Для электрона в водородоподобном атоме функция потенциальной энергии 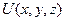 обладает центральной симметрией и задается выражением ,  

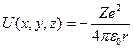где Z – число протонов в ядре (порядковый номер атома в таблице Менделеева);

Z e – заряд ядра ( е –  величина заряда электрона);

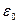− электрическая постоянная;

r – расстояние от ядра до точки (x, y, z).

Линейный гармонический осциллятор относится к одномерному случаю и потенциальная энергия задается выражением:

,  

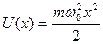где m −  масса частицы;

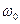 − собственная циклическая частота осциллятора;

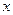 − координата частицы.

Для частиц в трехмерной или одномерной прямоугольной “потенциальной яме” с бесконечными прямоугольными стенками потенциальная энергия внутри “ямы” равна нулю ( 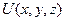= 0 или ).

 


⇐ Предыдущая1234Следующая ⇒
  

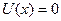© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.