Хелпикс

Главная

Контакты

Случайная статья



Интегрирование простейших правильных дробей

⇐ ПредыдущаяСтр 2 из 2


Интегрирование простейших правильных дробей

Рассмотрим методы интегрирования простейших дробей I, II, III типов.

I.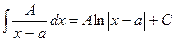

II.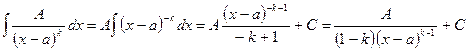

III.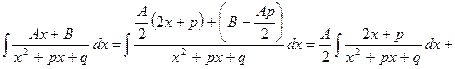

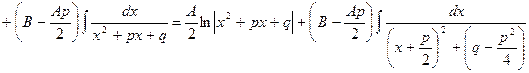
(подставляем в числитель производную знаменателя 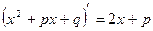 и в знаменателе второй дроби выделяем полный квадрат 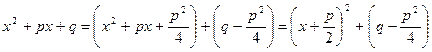, где 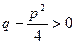, так как )

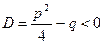Тогда

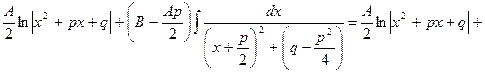
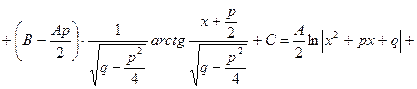
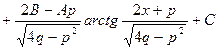
Пример:

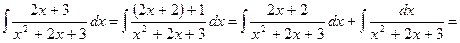
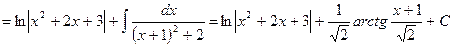
В данном случае производная знаменателя равна .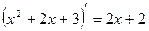

 

Интегрирование правильных дробей

Рассмотрим правильную дробь 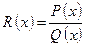, где 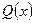 – многочлен степени n. Будем считать, что старший коэффициент в  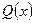равен единице. В курсе алгебры доказывается, что такой многочлен с действительными коэффициентами может быть разложен на множители первой и второй степени с действительными коэффициентами:

,

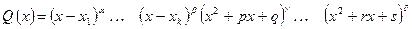где 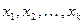 - действительные корни многочлена 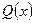, а квадратные трёхчлены не имеют действительных корней. Можно доказать, что тогда  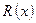представляется в виде суммы простейших дробей I-IV:

,

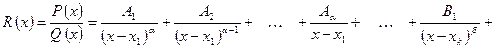
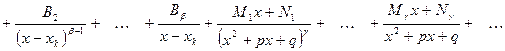
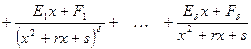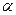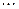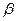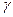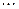где показатели у знаменателей последовательно уменьшаются от  до 1, , от  до 1, от  до 1, , от 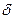 до 1, а 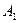, , 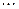 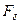- неопределённые коэффициенты.

 

Методы нахождения неопределённых коэффициентов

1) Метод частных значений:

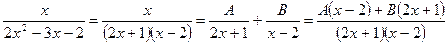
Тогда .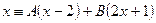

Придаём x переменной определённые значения (корни знаменателя) и находим коэффициенты A и B:

: ,

: ,

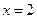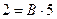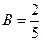
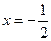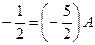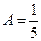
В качестве частных значений берём корни знаменателя, получаем:

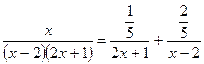
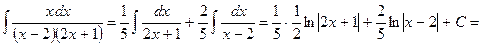
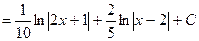
2) Метод сравнения коэффициентов:

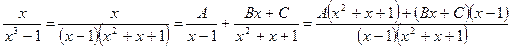
Получаем .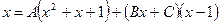

Даём x значение, равное действительному корню знаменателя:

: ,

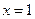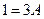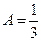
Сравниваем коэффициенты при одинаковых степенях x:

при : .

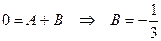при : .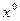

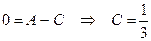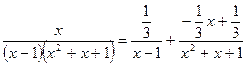
Получаем


⇐ Предыдущая12
  

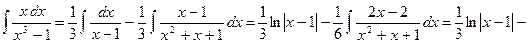
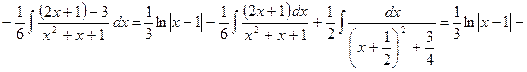
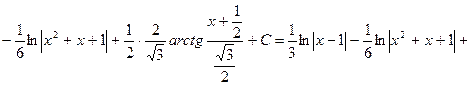
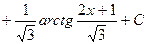
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.