ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ

Определение рациональных функций

Определение. Рациональной функцией называется отношение двух многочленов 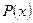и :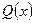

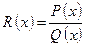где 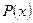- многочлен степени n, а 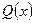– многочлен степени m.

Примеры:

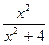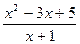1) ; 2) ; 3) .

Определение.Если степень числителя выше или совпадает со степенью знаменателя ( 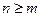), то дробь 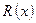называется неправильной, в противном случае ( 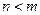) дробь 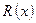называется правильной.

Примеры: 1-я и 2-я функции – неправильные дроби, 3-я функция – правильная дробь.

Интегрирование дробно-рациональных функций в конечном итоге сводится к интегрированию правильных дробей, так как неправильную дробь выделением целой части можно представить в виде суммы многочлена и правильной дроби.

Примеры:

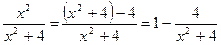
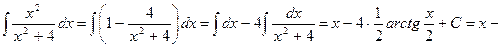
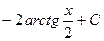
2) Выделяем целую часть делением в столбик, в результате чего получаем:

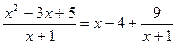
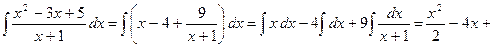
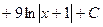
Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.

Определение. Правильные рациональные дроби вида

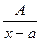
II.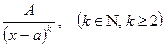

III. 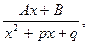(корни знаменателя комплексные, т.е. )

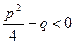IV. 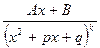, ( , 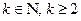корни знаменателя комплексные)

называются простейшими дробями I, II, III, IV типов. Никаких других простейших правильных дробей не существует.

12 Следующая ⇒